Kompendium > Betrieb der Leitung bei sinusförmiger Anregung > Verlustlose Leitung

Spannungsverteilung

Sind die Leitungsbeläge L', C' und damit der Wellenwiderstand und die Wellengeschwindigkeit v genau bekannt, kann man die Wellenlänge λ aus der Spannungsverteilung messen und daraus die Frequenz der Generatorspannung bestimmen (Gleichung (128))
(199)
Weiter lässt sich der Reflexionsfaktor am Leitungsende nach Betrag und Winkel aus der Spannungsverteilung ermitteln, woraus über die Beziehung
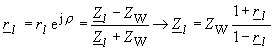(200)
Betrag und Winkel des Abschlusswiderstandes bekannt sind.
Über solche Messungen kann man z. B. Materialeigenschaften von Dielektrika bei hohen Frequenzen ermitteln.
Ausgangspunkt ist die Spannungsverteilung Gleichung (114) und der Zusammenhang nach Gleichung (148)
(114)
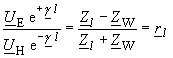(148)
Für = jβ und mit = rlejσ wird
(201)
Mit der Eulerschen Formel kann man zerlegen
(202)
und erhält für den Betrag der Spannung
(203)
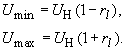Wegen -1cos(2β(l-x)-σ) +1 hat die Spannungsverteilung Spannungsminima und Spannungsmaxima (Bild 19):
(204)
Die sogenannte Welligkeit s und der Anpassungsfaktor m sind durch das Verhältnis dieser Spannungswerte definiert und liefern den Betrag des Reflexionsfaktors am Leitungsende:
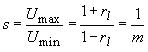(205)
(206)
Den Winkel σ des Reflexionsfaktors erhält man aus folgender Überlegung:
Es sei die Stelle des ersten Spannungsminimums vom Leitungsende gesehen d1, also x1 = l - d1. Damit gilt
(207)
und mit wird
(208)
Durch Ausmessen von d1 und λ ist der Winkel σ bestimmt. Nach Gleichung (200) lässt sich nun der Abschlusswiderstand nach Betrag und Winkel angeben.

Mit der Experimentierumgebung: "Betrieb der Leitung bei sinusförmiger Anregung" können die Spannungsverteilungen für unterschiedliche Lastfälle visualisiert werden. Empfehlenswert ist, für unterschiedliche Lastfälle die Messgrößen zu bestimmen und die Gleichungen (206) und (208) zu überprüfen.