Kompendium > Betrieb der Leitung bei sinusförmiger Anregung

Hauptwelle, Echowelle, Wellenparameter

Untersucht wird nun die Wellenausbreitung auf Leitungen mit linearen Leitungsbelägen R', L', C', G' bei sinusförmiger Spannungsquelle und linearen Wechselstromwiderständen für den Innenwiderstand der Quelle und den Abschlusswiderstand (Lastwiderstand) der Leitung (Bild 13). Mit diesen Vorgaben kann eine analytische Lösung der Einschaltvorgänge (t 0) im Allgemeinen nicht angegeben werden. Die Betrachtungen beschränken sich auf den sogenannten stationären Zustand (t → ∞). Bezüglich des Zeitverhaltens der elektrischen Größen kann davon ausgegangen werden, dass sie sich an allen Stellen der Leitung sinusförmig mit der Frequenz der Quellspannung ändern. Die Ergebnisse für den stationären Betrieb einer verlustlosen Leitung bei sinusförmiger Quellspannung
	(82)
	(83)
	(84)
	(85)
	(86)
	(87)
müssen als Sonderfall integriert sein. Das legt nahe, für die Spannungs- und Stromverteilung auf der verlustbehafteten Leitung ebenfalls von Haupt- und Echowellen auszugehen. Wegen des Widerstands- und Leitwertbelages der Leitung wird aber die Hauptwelle vom Anfang zum Ende der Leitung gedämpft, die Echowelle vom Ende der Leitung zum Anfang. Mit der Dämpfungskonstante α (α 0) der Leitung lautet der Lösungsansatz für die Haupt- und Echowellen (Bild 14):
	(94)
	(95)
	(96)
	(97)
Die Lösungsansätze für die Spannungs- und Stromhauptwelle und die Spannungs- und Stromechowelle werden in das Gleichungssystem zur Bestimmung der Orts-Zeitfunktionen u(x, t), i(x, t)
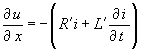	(10)
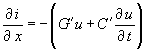	(11)
eingesetzt, um die Korrektheit der Ansätze zu prüfen. Differenzieren und addieren erfolgt zweckmäßig über die komplexen Orts-Zeitfunktionen:
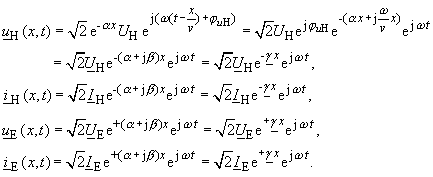	(98)
Dabei ist
	(99)
(also β > 0) die Phasenkonstante der Leitung und
	(100)
die (komplexe) Ausbreitungskonstante der Leitung. Mit den partiellen Ableitungen für die Hauptwellen
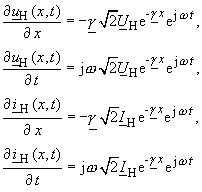	(101)
erhält man aus den Gleichungen (10), (11):
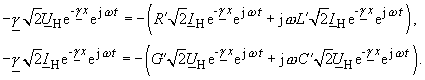	(102)
Da die Terme mit den e-Funktionen immer von Null verschieden sind, erhält man nach kürzen
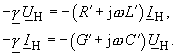	(103)
Die komplexe Ausbreitungskonstante folgt damit aus den Leitungsbelägen zu
	(104)
mit (α 0, β > 0). Für die sogenannte komplexe Wellenimpedanz folgt aus den obigen Gleichungen
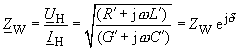	(105)
Mit den partiellen Ableitungen für die Echowellen
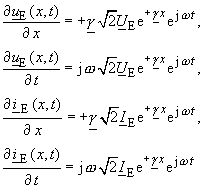	(106)
erhält man aus den Gleichungen (10), (11):
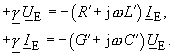	(107)
Die komplexe Ausbreitungskonstante folgt damit in Übereinstimmung mit Gleichung (104) zu
	(108)
Für die komplexe Wellenimpedanz folgt nun aus Gleichung (107)
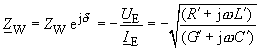	(109)
Damit erhält man die Spannungs- und Stromverteilungen:
	(110)
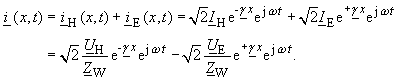	(111)
Mit der Vereinbarung
	(112)
(in Übereinstimmung auch mit den Betrachtungen zur verlustlosen Leitung) muss für die Stromverteilung geschrieben werden:
	(113)
Die 0rtsabhängigkeit der Spannungs- und Stromverteilung folgt zu
	(114)
	(115)
Im Zeitbereich lauten die Verteilungen:
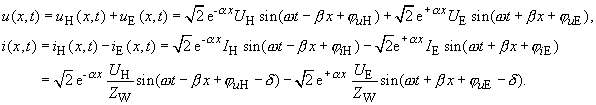	(116)
Die Lösungsansätze für den stationären Betrieb Gleichungen (94) bis (97) sind korrekt. Das Einsetzen in die Beschreibungsgleichungen des infinitesimalen Leitungselementes liefert zugleich die Wellenparameter komplexe Wellenimpedanz (mit der Einheit Ω)
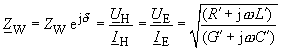	(117)
und komplexe Ausbreitungskonstante (mit der Einheit km-1)
	(118)
die aus den Leitungsbelägen berechnet werden können. Auch die Leitungsparameter Dämpfungskonstante α und Phasenkonstante β können unmittelbar aus den Leitungsbelägen berechnet werden. Aus Gleichung (118) erhält man
	(119)
und
	(120)
und damit
	(121)
	(122)
Die Konstanten werden mit der Leitungslänge l verrechnet zu dem Dämpfungsmaß α der Leitung
	(123)
dem Phasenmaß oder Übertragungswinkel b der Leitung
	(124)
und dem Übertragungsmaß der Leitung
	(125)
Ein weiterer wichtiger Parameter der Wellenausbreitung ist die Wellenlänge λ der Hauptwelle und Echowelle. Nehmen wir die Hauptwelle (vgl. Gleichung (116), ergibt sich die Wellenlänge für eine bestimmte Zeit t1 aus zwei Punkten der Leitung (x1, x1 + λ), die eine Phasendifferenz 2π haben (Bild 15):
	(126)
	(127)
Mit Gleichung (99) erhält man die Zusammenhänge
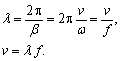	(128)
Dividiert man die Leitungslänge durch die Wellenlänge, erhält man die Anzahl der Phasendrehungen der Welle auf der Leitungslänge
	(129)