| Kompendium > Betrieb der Leitung bei sinusförmiger Anregung > Leitungsgleichungen | |
|
|
| Wir betrachten den Quotienten der komplexen Momentanwerte von Echowelle und Hauptwelle am Ende der Leitung: | |
 |
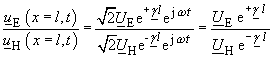(146) |
| Nun gilt aber auch am Leitungsende (Bild 16) | |
 |
(147) |
| Gleichung (147) liefert nach Umstellen | |
 |
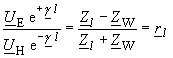(148) |
 ist
der komplexe Reflexionsfaktor am Leitungsende und ist wie der Vergleich
mit Gleichung (146) zeigt das Verhältnis des komplexen Momentanwertes
der Echowelle am Leitungsende zum komplexen Momentanwert der Hauptwelle
am Leitungsende: |
|
 |
(149) |
| Für den Leitungsanfang gilt nach Bild (16) | |
 |
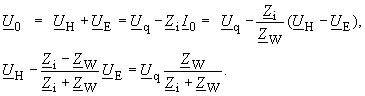(150) |
| Benennt man analog zu Gleichung (149) als komplexen Reflexionsfaktor am Leitungsanfang | |
 |
(151) |
| ist | |
 |
(152) |
| Aus den Gleichungen (148), (152) erhält man | |
 |
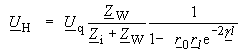(153) |
 |
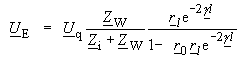(154) |
| Die Spannungs- und Stromverteilung lautet nun mit den Gleichungen (114), (115): | |
 |
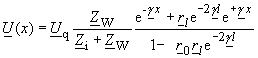(155) |
 |
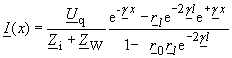(156) |
Damit kann die Spannungs- und Stromverteilung für
jeden Punkt der Leitung in Abhängigkeit von den Wellenparametern
Wellenimpedanz und komplexe Ausbreitungskonstante und von
den Parametern der Quelle und der Last angegeben werden. Mit der Experimentierumgebung „Betrieb der Leitung bei sinusförmiger Anregung“ können Sie für wählbare Leitungsbeläge, Leitungslänge, Frequenz der Generatorspannung und Lastbedingungen z.B. das Ausbreiten der Haupt- und Echowelle von Spannung und Strom auf der Leitung verfolgen und die Spannungs- und Stromverteilung auf der Leitung anzeigen lassen. |
|
|