Kompendium > Ergänzungen

Laplace-Transformation zur Analyse der Wellenausbreitung

Für die Analyse von Ausgleichsvorgängen ab t 0 bietet sich auch die Laplace-Transformation an (vgl. Lernprogramm Laplace-Transformation). Das Gleichungssystem (10), (11) zur Bestimmung der Orts – Zeitfunktionen u(x,t), i(x,t) lässt sich im Bildraum leicht nach den Bildfunktionen umstellen. Die Rücktransformation der Bildfunktionen in den Zeitraum gelingt jedoch nur für Spezialfälle.
Das hier zur Anwendung kommende Verfahren der Operatorimpedanzen setzt voraus, dass für t = -0 alle Energiespeicher im Netz leer sind (alle Kondensatoren ungeladen, alle Induktivitäten stromfrei, das heißt die Leitung muss stromfrei und spannungsfrei sein). Mit folgendem abgekürzten Verfahren können dann die Gleichungen für die Bildfunktionen aufgestellt werden:
Die Beschreibungsgleichungen werden mit den Regeln der symbolischen Methode aufgestellt, dann wird überall statt jω→ p eingesetzt und die komplexen Amplituden bzw. Effektivwerte der Erregungen und der gesuchten Größen werden durch die Bildfunktionen der Erregungen und der gesuchten Größen ersetzt.
Die Gleichungen (155), (156) sind aber die für das „Wechselstromnetzwerk“ nach Bild 16 aufgestellten Beschreibungsgleichungen:
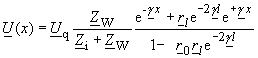(155)
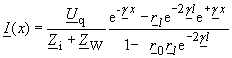(156)
die nun wie oben beschrieben in die Bildgleichungen U(x,p), I(x,p) umzusetzen sind, um dann durch Rücktransformation die Spannungs- und Stromverteilung u(x,t), i(x,t) zu erhalten.
Es ist für die Rücktransformation notwendig, den in den Gleichungen erkenntlichen Summenterm für die geometrische Reihe als Summe zu schreiben:
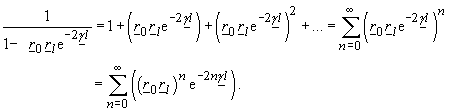(248)
Allerdings setzt das voraus
(249)
Die Vorgehensweise soll für bestimmte Parameterwerte demonstriert und mit bisherigen Ergebnissen verglichen werden.

Verlustlose Leitung mit ohmschen Widerständen Ri, Rl
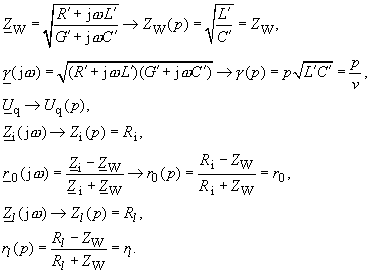Für die Wellenausbreitung auf verlustlosen Leitungen wird
(250)
Uq(p) steht als Bildfunktion für eine beliebige Anregung.
Damit erhält man mit der Signallaufzeit tL = die Bildgleichungen
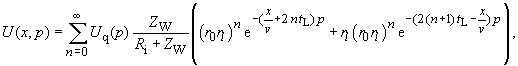(251)
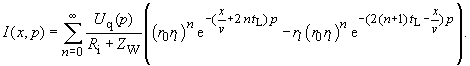(252)
Mit dem Verschiebungssatz der Laplace-Transformation
(253)
(die Laplace-Transformierte einer um t0(t0 > 0) nach rechts verschobenen Originalfunktion f(t - t0) mit f(t - t0) ≡ 0 für t < t0 ist gleich der Laplace-Transformierten der nicht verschobenen Originalfunktion f(t) , multipliziert mit dem Faktor )
folgen die Gleichungen im Orts-Zeitbereich
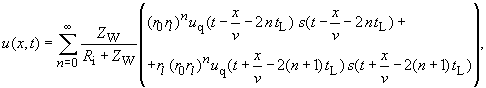(254)
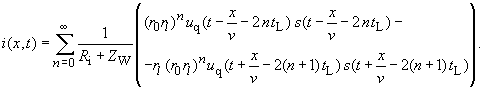(255)
Für das Einschalten einer Gleichspannung
(256)
wird aus dem Gleichungspaar (254), (255) die Lösung Gleichungspaar (61), (62).
Für das Einschalten einer Wechselspannung mit
(257)
wird aus dem Gleichungspaar (254), (255), die Lösung Gleichungspaar (77), (78).
Für die verlustlose Leitung und ohmsche Widerstände Ri, Rl lässt sich für jede beliebige Anregung uq(t) aus den Gleichungen (254), (255) die Spannungs- und Stromverteilung u(x,t), i(x,t) auf der Leitung angeben.

Verzerrungsfreie Leitung und ohmsche Widerstände Ri, Rl
Realisiert man durch entsprechende Gestaltung der Leitungsbeläge eine Leitung mit verzerrungsfreier Signalübertragung (vgl. Verzerrungsfreie Übertragung)
, (178)
ist in den Bildfunktionen nun im Unterschied zur verlustlosen Leitung zu berücksichtigen:
(258)
Damit lauten die Bildfunktionen für U(x,p), I(x,p)
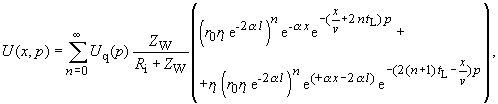(259)
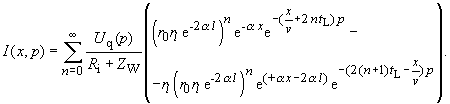(260)

Die Gleichungen im Orts- Zeitbereich für die Spannungs- und Stromverteilung lauten nun:

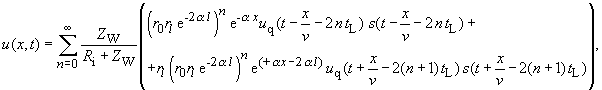(261)
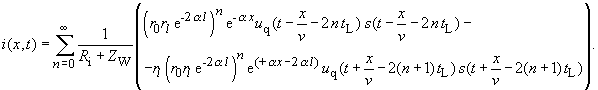(262)

Die Spannungs- und Stromwellen erfahren ortsabhängig eine zusätzliche Bedämpfung.
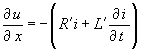Aus obigen Ergebnissen über den Bildbereich kann für den Zeitbereich gefolgert werden:
Für die aus dem Ersatzschaltbild des Leitungselementes abgeleiteten Beschreibungsgleichungen zur Bestimmung der Orts-Zeitfunktionen u(x,t), i(x,t)
(10)
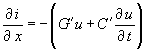(11)

können die Lösungsansätze
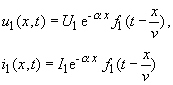(263)
mit festen Werten U1, I1 und f1 dimensionslos und beliebigem Profil und
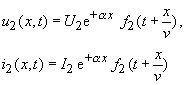(264)
verifiziert werden.
Einsetzen in die Gleichungen (10), (11) führt zu den Bedingungen für die Gültigkeit der Lösungsansätze
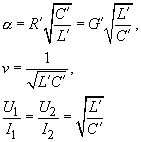(265)
Diese Bedingungen stimmen, wie gezeigt, überein mit der Anforderung an die Leitung zur Realisierung verzerrungsfreier Übertragung
(178)
Ohmsch-induktive und ohmsch-kapazitive Quellwiderstände und Leitungsabschlüsse
Die Laplace-Transformation ermöglicht auch einen Zugang zur Berechnung der Wellenausbreitung auf verlustlosen bzw. verzerrungsfreien Leitungen bei ohmsch-induktiven und ohmsch-kapazitiven Quellwiderständen und Leitungsabschlüssen.
Im Bildbereich ist nun zu berücksichtigen:
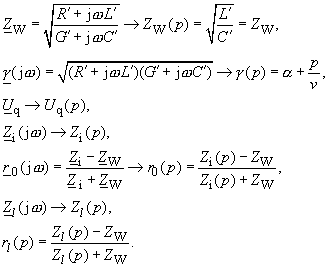(266)
Es ist einleuchtend, dass eine allgemeine Lösung wie z. B. Gleichungspaar (254), (255) nicht angegeben werden kann. Jeder Summand muss für sich nach den Regeln der Laplace-Transformation in den Zeitbereich zurück transformiert werden.
Beispielsweise folgt für das Aufladen eines Kondensators über eine verlustlose Leitung mit den Parametern ZW, v, l, tL bei reflexionsfreier Einspeisung einer Gleichspannung Uq:
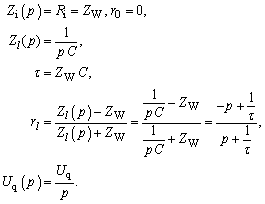(267)
Damit lauten die Bildfunktionen:
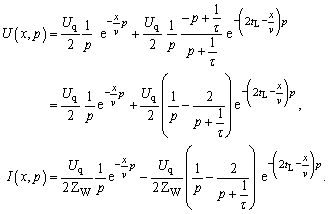(268)
Die Rücktransformation in den Zeitbereich führt zur Spannungs-Stromverteilung:
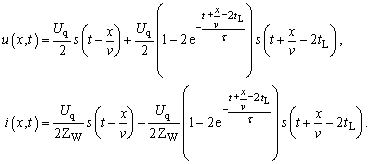(269)
Im Beispiel 7 wird die Berechnung des Aufladevorganges für Quellwiderstände Ri ≠ ZW erläutert.