| Kompendium > Ergänzungen | |
| Die Berechnung der Leitungsbeläge einer Dreiphasen -
oder Drehstromleitung kann zurückgeführt werden auf die Betrachtung
einer Einphasenleitung mit Sternspannung und Außenleiterstrom. Kapazitätsbelag Für symmetrischen Leitungsaufbau liegen die Teilkapazitäten C0, C1 (Bild 25) zwischen den Außenleitern bzw. zwischen den Außenleitern und Neutralleiter. Die Kapazitäten können durch Messung oder Rechnung bestimmt werden. Der kapazitive Stromanteil im Außenleiter 1 beträgt |
|
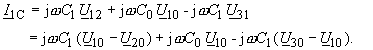 |
(270) |
| Wegen |
|
| (271) | |
| Damit beträgt der Kapazitätsbelag der Einphasenleitung 1,0 | |
| (272) | |
| Leitwertbelag Für den Leitwertbelag gilt entsprechend |
|
| (273) | |
| Induktivitätsbelag Bei symmetrischer Last mit |
|
| (274) | |
| führt der Neutralleiter den Rückstrom Null. Nur die Außenleiterströme liefern Beiträge zum verketteten Magnetfluss in der Leiterschleife 1,0 (Bild 25): | |
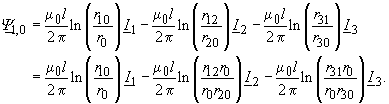 |
(275) |
| Mit Gleichung (274) und r10
= r20 = r30
sowie r12
= r23 = r31
und r0 = |
|
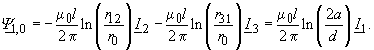 |
(276) |
| Beim Induktivitätsbelag der Einphasenleitung 1,0 ist die „innere“ Induktivität des Außenleiters 1 zu berücksichtigen: | |
| (277) | |
| Widerstandsbelag Für den Widerstandsbelag der Dreiphasenleitung ist der Widerstand eines einzelnen Außenleiters einzusetzen. Im Beispiel 8 wird die Spannungs- und Stromverteilung auf einer Drehstromfreileitung betrachtet. |
|