| Allgemein kann man sagen: je glatter der Funktionsverlauf
ist, desto schneller konvergiert die Fourier-Transformierte bzw. die Fourier-Reihe.
Als Beispiele seien angeführt: |
| Rechteckimpuls |
|Ck| ˜
1/k |
(Funktion hat eine Sprungstelle) |
| Dreieckimpuls |
|Ck| ˜
1/k2 |
(1.Ableitung hat eine Sprungstelle) |
| cos2-Impuls |
|Ck| ˜
1/k3 |
(2.Ableitung hat eine Sprungstelle) |
|
| Zum Schluß dieses Teils soll nochmals das Faltungsprodukt
betrachtet werden. Man kann die Fourier-Transformierte eines Faltungsproduktes
mittels der Ideen des Impulsverfahrens berechnen. Nach dem Faltungssatz
gilt für ein Faltungsprodukt im Zeitbereich im Frequenzbereich ein
normales Produkt. |
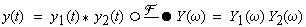 |
(6-44) |
| Ziel ist es, die Differentiation wieder im Zeitbereich anzuwenden,
um im Frequenzbereich die Gleichung (6-38) benutzen zu können. Dazu
wird folgender "Trick" im Frequenzbereich angewendet, man erweitert
das Produkt mit j ω |
 |
(6-45) |
| Die Rücktransformation in den Zeitbereich liefert mit
dem Differentiations- und dem Integrationssatz |
 |
(6-46) |
| Wenn es gelingt, die Funktion y1(t)
solange zu differenzieren, bis nur noch Diracimpulse und Ableitungen dieser
Impulse auftreten, kann man die Faltung durch Verschiebung und Überlagerung
von Funktionen vornehmen. Dabei muß sich allerdings y2(t)
mit "vernünftigen" Aufwand integrieren lassen. |
 |