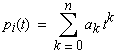| Der Vorgang der Transformation mittels der Impulsmethode wird
im folgenden in allgemeiner Form beschrieben. |
| Zunächst ist der Impuls bzw. die Ausgangsfunktion in
Form einer Gleichung zu beschreiben, wobei man mittels der Sprungfunktion
σ(t) Unstetigkeitsstellen bzw. Ausschnitte
von Funktionen definiert. Zum Beispiel kann man durch Multiplikation der
Funktion y(t) mit σ(t
- α) - σ(t
- β) den Definitionsbereich der
Funktion auf das Intervall [α, β]
beschränken, also aus der Funktion den Bereich "herausschneiden",
der in diesem Intervall definiert ist. Handelt es sich bei der zugrundeliegenden
Funktion um ein Polynom, dann ist die Impulsmethode anwendbar und die Funktion
ist etwa in folgender Form darzustellen: |
 |
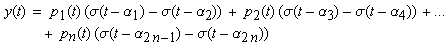(6-34) |
| mit |
 |
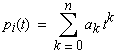(6-35) |
Polynom vom Grad n und αi
αi+1. Die so beschriebene
Funktion y(t) ist nun zu differzieren, wobei
man für jeden Summanden yi(t)
aufgrund der Produktregel errechnet: |
 |
(6-36) |
| Zunächst ist der Vorfaktor bei der Diracfunktion auszuwerten,
da die Funktion nur an einer Stelle ungleich Null ist und deshalb die Funktion
pi(t) an dieser Stelle keine Abhängigkeit
mehr von t besitzt, also eine Konstante darstellt.
Es ergibt sich |
 |
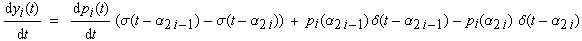(6-37) |
| In dieser Art ist die Funktion y(t)
bzw. sind ihre Teilfunktionen yi(t)
weiter zu differenzieren, bis auf der rechten Seite der Funktion nur noch
Diracfunktionen, und deren Ableitungen auftreten. Mittels der beiden Gleichungen
(6-29) und (6-33)
läßt sich dann die Fourier-Transformierte der Zeitfunktion y(t)
berechnen. |
