Kompendium > Anwendung der Fouriertransformation
Kompendium > Anwendung der Fouriertransformation |
|
|
|
| Jetzt läßt sich die Fourier-Transformierte berechnen: | |
| (6-11) | |
 |
(6-12) |
 |
(6-13) |
| Um die Fourier-Transformierte der Ausgangsfunktion zu erhalten, muß der Konvergenzfaktor wieder eliminiert werden. Dazu bildet man den Grenzübergang α → 0 und es ergibt sich die Fourier-Transformierte der Signumfunktion | |
 |
(6-14) |
 |
(6-15) |
| Der Grenzübergang liefert ein Ergebnis, das für ω ≠ 0 gültig ist. Da es sich um eine ungerade Zeitfunktion handelt, ist der Gleichanteil Null. Es gilt: | |
 |
(6-16) |
| Bild 6-2 zeigt das Amplitudenspektrum der Signumfunktion. | |
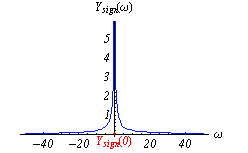 Bild 6-2 Amplitudenspektrum der Signumfunktion |
|
