| Um die Impulsmethode anwenden zu können, benötigt
man die Ableitungen der Fourier-Transformierten allgemeiner und speziell
der Diracfunktion. Allgemein gilt für die Fourier-Transformierte: |
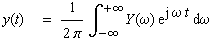 |
(6-26) |
| Die n-malige Differentiation nach der Zeit liefert |
 |
(6-27) |
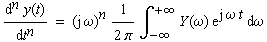 |
(6-28) |
| Aus dieser Gleichung läßt sich für die Fourier-Transformierte
der n-ten Ableitung folgern: |
 |
(6-29) |
| Wie bereits oben erwähnt, benötigt man ebenso die
Fourier-Transformierte der Ableitung des Diracimpulses. Aufgrund der Gleichung
(6-29) erhält mit |
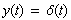 |
(6-30) |
| und |
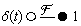 |
(6-31) |
| die Beziehung |
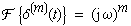 |
(6-32) |
| Zusammen mit den Verschiebungssatz
ergibt sich |
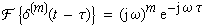 |
(6-33) |