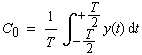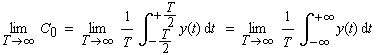| Zur Existenz des Fourier-Integrals bzw. der Spektralfunktion
Y(ω) kann man eine hinreichende, aber
nicht notwendige Bedingung aus der Entwicklung entnehmen. Der Übergang
von den diskreten Frequenzen n ω0
zur kontinuierlichen Frequenz ω wurde
über die komplexen Fourier-Koeffizienten Cn
geführt, dabei tritt auch C0
auf, für das gilt: |
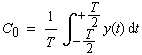 |
(1-23) |
| => |
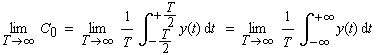 |
(1-24) |
| Dieser Grenzwert existiert, wenn das Integral existiert und
endlich ist. Man kann zeigen, daß die absolute Integrierbarkeit der
Funktion y(t) |
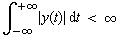 |
(1-25) |
| eine hinreichende Bedingung für die Existenz der Spektralfunktion
Y(ω) ist. Diese Bedingung erfüllen
zum Beispiel Signale mit endlicher Energie. Anderseits ist zum Beispiel
die Funktion |
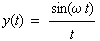 |
(1-26) |
| nicht absolut integrierbar, obwohl das Fourier-Integral dieser
Funktion existiert, deshalb handelt es sich bei der obigen Beziehung nur
um eine hinreichende Bedingung. |
| Der Betrag der Fourier-Transformierten |Y(ω)|
ergibt das Amplitudenspektrum oder die Amplitudendichte von y(t).
Der Winkel arg{Y(ω)} stellt das Phasenspektrum
dar. Aus der Definition des Fourier-Integrals (Gleichung
(1-15)) erkennt man, daß für rein reelle Zeitfunktionen y(t)
die Fourier-Transformierte des negativen Arguments gleich der konjugiert
komplexen Fourier-Transformierten ist: |
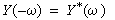 |
(1-27) |


|