| Eine periodische Zeitfunktion besitzt ein Spektrum aus diskreten
Spektrallinien, die einen Abstand |
 |
(1-1) |
| bzw. |
 |
(1-2) |
| besitzen, wobei Τ die Periode
der Funktion bedeutet. Offenbar rücken die Spektrallinien mit größerer
Periode immer dichter zusammen. Für den Grenzfall eines einmaligen
Zeitvorgangs gibt es keine diskreten Frequenzen mehr: |
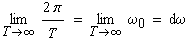 |
(1-3) |
| bzw. |
 |
(1-4) |
| Nun kann einer einzelnen Frequenz keine Amplitude mehr zugeordnet
werden, da das Signal sonst bei unendlich vielen Spektrallinien mit endlicher
Energie eine unendlich große Energie besitzen würde. Es ergibt
sich ein kontinuierliches Frequenzspektrum |
 |
(1-5) |
| bzw. |
 |
(1-6) |
| Das heißt, es treten nicht nur bestimmte diskrete Frequenzen
auf, wie bei der Fourier-Reihe, sondern jede beliebige Frequenz von 0 bis
∞. Dieser Ansatz bedeutet für die Periode der Fourier-Reihe,
daß die "primitive" Periode Τ
= 2π/ω0 gegen ∞
strebt. |