| Das Fourier-Integral einer Zeitfunktion y(t
) ist erklärt durch: |
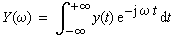 |
(1-15) |
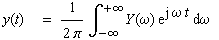 |
(1-16) |
| Y(ω) nennt man die Spektralfunktion
oder Fourier-Transformierte oder Spektraldichte oder Frequenzfunktion von
y(t). |
| Dabei nennt man die Darstellung der Funktion y(t)
mittels ihrer Fourier-Transformierten die Umkehrtransformation. |
| Für die Frequenz f ergibt
sich: |
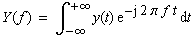 |
(1-17) |
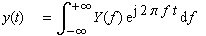 |
(1-18) |
| Dieser Zusammenhang kann aus der Darstellung der komplexen
Fourier-Koeffizienten auch durch folgende Überlegung gewonnen werden: |
| Da nur einem differentiell kleinem Frequenzbereich der Breite
d f eine Energie zugeordnet werden kann, gilt |
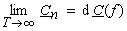 |
(1-19) |
| Das Differential d C(f)
repräsentiert den Amplitudenanteil in der differentiell kleinen Umgebung
der Frequenz |
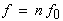 |
(1-20) |
| Mit dem Grenzübergang Τ
→ ∞ erhält man: |
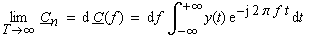 |
(1-21) |
| Mit der Definition der Amplitudendichte |
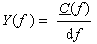 |
(1-22) |
| folgt die obige Beziehung. |