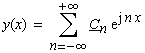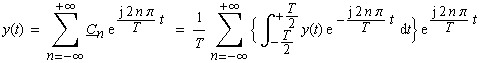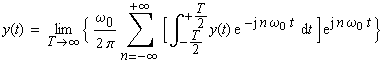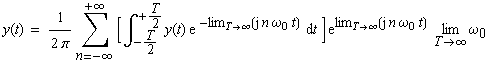| In der komplexen Darstellung der Fourier-Reihe läßt
sich der Grenzübergang wie folgt formulieren: |
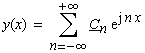 |
(1-7) |
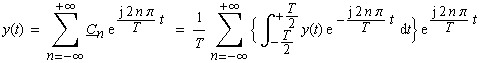 |
(1-8) |
| Benutzt man die Beziehung |
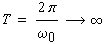 |
(1-9) |
| bzw. |
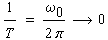 |
(1-10) |
| dann folgt für die Darstellung der Funktion y(t),
die aufgrund dieses Grenzwertes für die Periode Τ
jetzt nicht mehr eine periodische Funktion ist: |
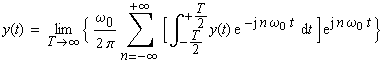 |
(1-11) |
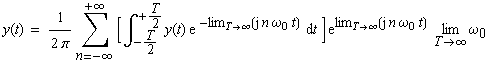 |
(1-12) |
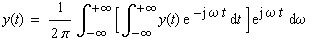 |
(1-13) |
| Durch den Grenzübergang Τ
→ ∞ bzw. n ω0
→ω geht die Summation der Anzahl
n der Oberwellen der Grundfrequenz ω0
in eine Integration der kontinuierlichen Frequenz ω
über. Betrachtet man die Frequenz f anstatt
die Kreisfrequenz ω, dann folgt: |
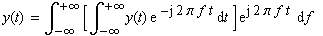 |
(1-14) |
| Das Ergebnis des jeweils inneren Integrals stellt eine Funktion
der Frequenz ω bzw. f
dar, deshalb definiert man: |