Nullstellengleichungen

Wie lassen sich nährungsweise die Nullstellen von nichtlinearen Funktionen bestimmen?

Mögliche elektrotechnische Fragestellung

  • Bei der näherungsweisen Berechnung des Arbeitspunktes bei Diodenkennlinien setzt man beispielsweise die Spannungsgleichungen (Funktionsgleichungen) von Quelle und Diode gleich, um die Klemmenspannung \( U \) auszurechnen. Analog verfährt man mit den Stromgleichungen.

Notwendige mathematische Grundlagen

  • Das führt auf sogenannte „Nullstellengleichungen“ \( f(x) = 0 \), wobei die Funktion \( f(x) = 0 \) aus verschiedenen Funktionstypen besteht und sich damit die Nullstellen nicht elementar bestimmen lassen. Durch die Anwendung der Differentialrechnung kann man die Nullstellen mittels „NEWTON-Verfahren“ oder anderer Näherungsverfahren mit hinreichender Genauigkeit bestimmen.

Aufgabe

Die Anwendung des NEWTON-Verfahrens bei elektrotechnischen Sachverhalten soll hier am Beispiel einer Zusammenschaltung von einer Si-Halbleiterdiode mit einer linearen Spannungsquelle (Siehe Abbildung) betrachtet werden.

Dazu soll mittels analytischem Näherungsverfahren der Arbeitspunkt der Halbleiterdiode (Klemmenspannung \( U \) und Klemmenstrom \( I \)) mit einer Genauigkeit von \( 10^{-2} \) berechnet werden.

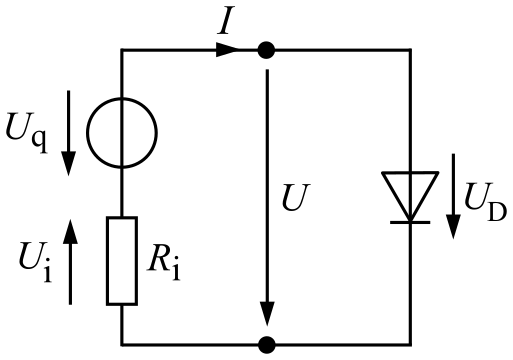
Halbleiterdiode als Verbraucher

Gegeben sind folgende Parameter:

  • Kenngrößen der Spannungsquelle:

\( U_\mathrm{q} = 1 \, \mathrm{V} \)
\( R_\mathrm{i} = 50 \, \mathrm{Ω} \)
  • Kenngrößen der Siliziumdiode:

\( I_\mathrm{S} = 1 \, \mathrm{pA} \)
\( \mathrm{m}·U_\mathrm{T} = 25 \, \mathrm{mA} \)

Lösungavariante:

Mittels NEWTON-Verfahren lässt sich der Arbeitspunkt wie folgt berechnen:

Die Stromgleichung für den Spannungsquellen-Zweipol

\( I = \dfrac{U_\mathrm{q}}{R_\mathrm{i}} - \dfrac{1}{R_\mathrm{i}}·U \)

und die Stromgleichung für die Diode

\( I = I_\mathrm{S} · \left[ \mathrm{e}^{\dfrac{U}{\mathrm{m}·U_\mathrm{T}}} - 1 \right] \)

werden gleichgesetzt.

Daraus ergibt sich die Nullstellengleichung

\( f(U) = 0 = \dfrac{U_\mathrm{q}}{R_\mathrm{i}} - \left[ \dfrac{1}{R_\mathrm{i}}·\mathrm{U} \right] - I_\mathrm{S} · \left[ \mathrm{e}^{\dfrac{U}{\mathrm{m}·U_\mathrm{T}}} - 1 \right] \)

für die gesuchte Klemmenspannung \( U \).

Hier ist also die Nullstelle einer Funktion \( f(U) \) zu bestimmen, die sich aus einer linearen und einer Exponentialfunktion zusammensetzt. Das gelingt nur mit analytischen oder numerischen Näherungsverfahren oder grafischen Lösungsmethoden.

Bei Anwendung des NEWTON-Verfahrens ergibt sich folgender möglicher Lösungsweg:

Die Formel

\( x_{n + 1} = x_n - \dfrac{f(x_n)}{f'(x_n)} \), mit \( n=1,2,3,... \)

übertragen auf das elektrotechnische Problem lautet dann:

\( U_{n + 1} = U_n - \dfrac{f(U_n)}{f '(U_n)} \)
mit: \( U_n = \) Startwert
\( U_{n+1} = \) verbesserter Startwert

Die erste Ableitung \( f '(U) \) ergibt sich durch Anwendung der Summenregel, Faktorregel und Kettenregel der Differentialrechnung zu

\( f'(U) = \dfrac{\mathrm{d}f}{\mathrm{d}U} = - \dfrac{1}{R_i} - \dfrac{1}{\mathrm{m}·U_\mathrm{T}} · I_\mathrm{S} · \mathrm{e}^{\dfrac{U}{\mathrm{m}·U_\mathrm{T}}} \)

Somit folgt für die erste Näherung:

\( U_{n + 1} = U_n - \dfrac{f(U_n)}{f '(U_n)} = U_n - \dfrac{ \dfrac{U_\mathrm{q}}{R_\mathrm{i}} - \dfrac{U_n}{R_\mathrm{i}} - I_\mathrm{S} · \left[ \mathrm{e}^{\dfrac{U_n}{\mathrm{m}·U_\mathrm{T}}} - 1 \right] }{ - \dfrac{1}{R_i} - \dfrac{1}{\mathrm{m}·U_\mathrm{T}} · I_\mathrm{S} · \mathrm{e}^{\dfrac{U_n}{\mathrm{m}·U_\mathrm{T}}} } \)

Einsetzen aller Werte liefert bei einem gewählten Startwert \( U_n = 0{,}6 \, \mathrm{V} \) einen verbesserten Näherungswert

\( U_{n+1} = 0{,}58 \, \mathrm{V} \)

Setzt man diesen verbesserten Wert als neuen Startwert \( U_n \) in die Näherungsformel ein, so erhält man nach endlicher Rechnung

\( U_{n+1} = 0{,}573 \, \mathrm{V} \)

Setzt man diesen verbesserten Wert als neuen Startwert \( U_n \) in die Näherungsformel ein, so erhält man nach endlicher Rechnung

\( U_{n+1} = 0{,}572 \, \mathrm{V} \)

Damit ist die geforderte Genauigkeit für die Klemmenspannung \( U \) erreicht.

Der Klemmenstrom \( I \) ergibt sich mit

\( I = \dfrac{U_\mathrm{q}}{R_\mathrm{i}} - \dfrac{1}{R_\mathrm{i}}·U = 8{,}56 \, \mathrm{mA} \)

Bemerkung: Von der Wahl eines geeigneten Startwertes hängt die Konvergenzgeschwindigkeit des Näherungswertes gegen die exakte Nullstelle ab.