Gleichungssysteme
Wie wird das lineare Gleichungssystem ausgewertet?
Notwendige mathematische Grundlagen:
Das zu lösende Gleichungssystem lautet mit Papier und Stift:
\( \begin{array}{lrrrrrrrrr}
(1) & \hspace{8pt} 60 \, \mathrm{Ω} & = & \red{1} & · & R_1 & + & \red{1} & · & R_1 \\
(2) & 0 & = & \red{α_1} & · & R_1 & + & \red{α_2} & · & R_2
\end{array} \)
mit:
\( \red{α_1}=4,0·10^{-5}\mathrm{K}^{-1} \) und \( \red{α_2}=-1,0·10^{-5}\mathrm{K}^{-1} \)
Lösung z.B. mit Einsetzungsverfahren:
Gleichung (1) nach \( R_2 \) auflösen und in Gleichung (2) einsetzen liefert \( R_1=12 \, \mathrm{Ω} \) und \( R_2=48 \, \mathrm{Ω} \).
Besser geht es, besonders bei komplizierten Berechnungen, mittels Mathcad.
Die Schrittfolge zeigt Ihnen, wie Sie das lineare Gleichungssystem einfach berechnen können und sollte Sie motivieren, zukünftige Berechnungen mit diesem leistungsfähigen Ingenieurwerkzeug effektiv durchzuführen:
Die Matrizenschreibweise des Gleichungssystems lautet:
\( \vec{\mathrm{R}}=\mathrm{M}·\vec{\mathrm{v}} \)
mit
\( \vec{\mathrm{R}} \) → Lösungsvektor
und
\( \mathrm{M} = \begin{bmatrix} 1 & 1 \\ {α_1} & α_2 \end{bmatrix} \) → Koeffizientenmatrix
und
\( \mathrm{v} = \begin{bmatrix} 60 \\ 0 \end{bmatrix} \) → Spaltenvektor (linke Seite des Gleichungssystems)
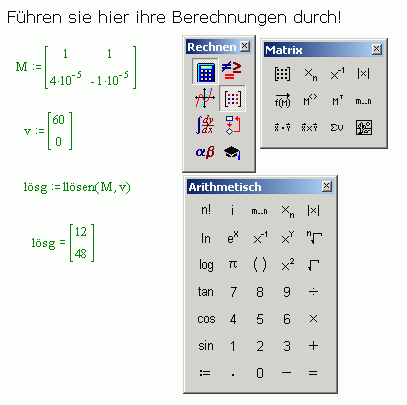
Arbeiten Sie parallel in dem Mathcad Fenster nach diesem Handlungsablauf:
- Schritt: Mathcad aufrufen,
- Schritt: Ansicht, Symbolleiste, Rechnen, Taschenrechner, Matrix, griechisch,
- Schritt: Definieren Sie die Koeffizientenmatrix \( \mathrm{M} \) als 2,2 Matrix und tragen Sie die Werte des Gleichungssystems ein,
- Schritt: Definieren Sie den Spaltenvektor \( \vec{\mathrm{v}} \) der linken Seite des Gleichungssystems als 2,1 Matrix,
- Schritt: Eingabe : lösg := llösung (\( \mathrm{M}, \mathrm{v} \)),
- Schritt: lösg = liefert Ihnen die Lösung.
Hier die Mathcad-Lösung von Aufgabe 8.1.6 aus dem Lernprogramm Grundstromkreis: