Wiederholung des NEWTON Verfahrens
Das NEWTON-Verfahren oder auch Tangentennäherungsverfahren dient
der schrittweisen Berechnung von Nullstellen beliebiger auf einem Intervall
\( I \) differenzierbarer Funktionen. Es gehört
zu den Iterationsverfahren in der Analysis.
Es ist also die "Nullstellengleichung" \( f (x) = 0 \) zu lösen.
Ausgehend von einem Anfangswert oder Startwert \( x_n = 0 \) konvergiert unter bestimmten Voraussetzungen die Folge der Tangentennullstellen mit
nach endlich vielen Rechenschritten gegen die exakte Nullstelle von \( f (x) = 0 \).
Die Näherungsformel entsteht aus der Taylorreihe
wobei \( a \) ein geschätzter Näherungswert
einer exakten Lösung \( a_0 \)
ist, der um \( h \) von der Lösung \( x_0 \)
entfernt ist, also \( x_0 = a + h \).
Bricht man die Taylorreihe nach dem 2. Glied ab, setzt \( a = x_0 \)
und \( a + h = x_{n+1} \)
und löst nach \( x_{n+1} \) auf, erhält man die Näherungsformel.
Beispiel:
| Gegeben: | \( f (x) = 1 - \mathrm{x} - \mathrm{e}^x \; \), \( x \in ℝ \) |
| Gesucht: | \( f (x) = 0 \) |
| Lösung: | \( 0 = 1 - x - \mathrm{e}^x \) |
Die „Nullstellengleichung“ lässt sich mit elementaren Mitteln nicht lösen. Durch probieren findet man hier leicht die exakte Nullstelle \( x_0 = 0 \) als Lösung oder mit Mathcad die graphische Lösung \( x_0 = 0 \) (vgl. Abb).
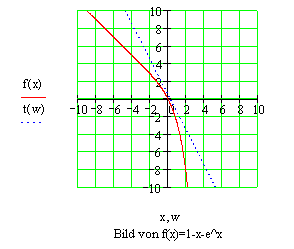
Mittels Tangentennäherungsverfahren oder NEWTON-Verfahren gelangt
man ebenfalls zu dem gleichen Ergebnis mit hinreichender Genauigkeit.
Als Startwert für das NEWTON-Verfahren wählen wir eine Stelle
rechts von der vermuteten exakten Nullstelle, z.B. \( x_n = 0{,}01 \)
Legen wir durch den Punkt \( P(x_n ; f (x_n)) \)
eine Tangente an das Bild von \( f (x) \),
so schneidet diese die \( x \)-Achse an der Stelle
\( x_n \).
Die Berechnung dieser Stelle erfolgt durch
Mit
und
folgt
Legen wir durch den Punkt \( P(x_{n+1} ; f (x_{n+1})) \),
eine Tangente an das Bild von \( f (x) \), so schneidet diese die \( x \)-Achse an der Stelle
\( x_{n+2} \).
Die Berechnung dieser Stelle erfolgt durch
Also
Nach endlich vielen Schritten konvergiert die Folge der Tangentennullstellen gegen die exakte Nullstelle von \( f (x) \), hier \( x = 0 \).
Die gleiche Rechnung lässt sich rationeller mittels Mathcad durchführen
Schnelle Lösung der Nullstellengleichung \( f (x) = 0 \) mit Mathcad

