Übertragungsverhalten

Periodische Vorgänge

Die Bildfunktion X(p) einer periodischen Erregung x(t -nT) erhält man aus der Bildfunktion X_E(p) der Erregung x_E(t) über dem Grundintervall T und dem Periodisierungsfaktor:

(95)

Mit der Übertragungsfunktion H(p) erhält man die Bildfunktion Y(p) der Systemantwort y(t):

(96)

Man ermittelt zunächst die Antwort auf den Impuls über der Grundperiode

(97)

und erhält die Systemantwort mit dem Verschiebungssatz

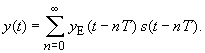(98)

Flüchtiger und stationärer Anteil der Systemantwort

Für die Untersuchung des Übertragungsverhaltens zerlegt man die Systemantwort in den flüchtigen und stationären Anteil:

(99)

Dabei gilt wegen

	(100)
	(101)

Für die Bildfunktionen gilt also:

(102)

Bekanntlich lässt sich bei periodischen Erregungen in LTI-Systemen die stationäre Lösung durch eine komplexe Fourier-Reihe beschreiben (vgl. Lernprogramm Fourier-Reihe):

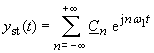(103)

mit

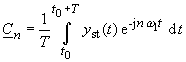(104)

und

(105)

Die Bildfunktion der stationären Lösung ist also

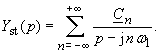(106)

Die einfachen Polstellen (Nullstellen im Nenner) p_n = jnω₁ liegen auf der imaginären Achse (Bild 14) und sind übereinstimmend mit Gleichung (102) die Wurzeln der Gleichung

(107)

Man erhält:

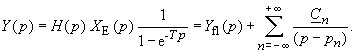(108)

Die Fourier-Koeffizienten C_n können mit der Grenzwertmethode bestimmt werden:

(109)

wobei der Grenzwert

(110)

mit der Bernoulli-L´Hospitalschen Regel ausgewertet wird.

Beispiel