Rücktransformation in den Originalraum

Grenzwertmethode/Einsetzverfahren

Bei einfachen reellen Nullstellen p₁, p₂, ..., p_n kann der Koeffizientenvergleich umgangen werden.

Betrachtet man Gleichung (73), so können A₁ und A₂ durch geeignete p-Werte unmittelbar bestimmt werden. So folgt mit der Wahl p = p₁ sofort A₁ und mit p = p₂ sofort A₂, wie im Ergebnis der Auflösung des Gleichungssystems Gleichung (74).

Verallgemeinert lautet die Vorgehensweise:

multipliziere zur Bestimmung von A_i die Bildfunktion mit (p - p_i):

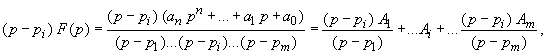(76)

setze p = p_i um alle A außer A_i zu eliminieren

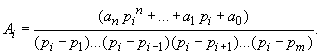(77)

Grenzwertmethode:

Da p_i (i = 1, 2, ..., m) Wurzel des Nennerpolynoms ist, ist die linke Seite der Gleichung (76) ein unbestimmter Ausdruck der Form 0 / 0, zu dessen Auswertung die Bernoulli-L'Hospitalsche Regel verwendet wird:

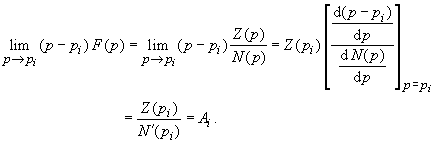(78)

Die Zeitfunktion f(t) zur Bildfunktion F(p) folgt dann aus:

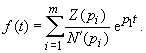(79)

(Heavysidescher Entwicklungssatz)

Das Einsetzverfahren ist im Fall einfacher reeller Nullstellen erfolgreich anzuwenden. Bei mehrfachen reellen Nullstellen und komplexen Nullstellen wird der Koeffizientenvergleich und das Auflösen des Gleichungssystems zur Bestimmung der A, B, C empfohlen.

Hinweis