Rücktransformation in den Originalraum

Partialbruchansatz

Wenn die Bildfunktionen der Erregungen in linearen Netzen mit konzentrierten Bauelementen rationale Funktionen sind (konstanter, potenzieller, exponentieller, harmonischer Verlauf), dann sind die Bildfunktionen der gesuchten Größen gebrochen rationale Bildfunktionen

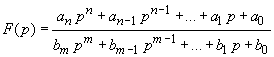(68)

mit reellen Koeffizienten a₀, a₁, ... , a_n, b₀, b₁, ... , b_n und in der Regel n < m (echt gebrochen rationale Funktionen).

Für n ≥ m kann F(p) durch Polynomdivision in ein Potenzpolynom und eine echt gebrochene rationale Funktion zerlegt werden.

Jeder echte Bruch (n < m) kann aber eindeutig in eine Summe von Partialbrüchen zerlegt werden. Der Koeffizient der höchsten Potenz im Nenner b_m wird dazu auf den Wert eins gebracht, indem Zähler und Nenner des Bruches durch b_m dividiert werden. Die Wurzeln der Gleichung Q(p) = 0 des so entstehenden Nennerpolynoms Q(p) bestimmen die Form der Zerlegung. Wegen der reellen Koeffizienten (a_v, b_v) in den Polynomen treten komplexe Nullstellen jeweils konjugiert komplex auf, die zu einem quadratischen Ausdruck zusammen gefasst werden. Die einzelnen Terme des Partialbruchansatzes werden mittels Korrespondenztafeln in den Originalraum zurück transformiert.

Beispiel: Nennerpolynom ist eine quadratische Funktion. Klassifikation der Lösung Q(p) = 0:

zwei verschiedene reelle Nullstellen p₁, p₂:

(69)

eine doppelte reelle Nullstelle p₁:

(70)

zwei konjugiert komplexe Nullstellen p₁ = -δ + jω, p₂ = -δ - jω:

(71)

Beispiel: Nennerpolynom ist eine kubische Funktion.