Rücktransformation in den Originalraum
Rücktransformation in den Originalraum |
|
|
|
Die mit dem Partialbruchansatz gleichgesetzte Bildfunktion wird mit dem Nennerpolynom der Bildfunktion durchmultipliziert, sowie die rechte Seite nach Potenzen von p geordnet. Gleichsetzen der Koeffizienten vor gleichen Potenzen von p im Zähler der linken und rechten Seite führt auf das Gleichungssystem zur Bestimmung der A, B, C im Partialbruchansatz.
Beispiel: Gleichung (69)
 |
(72) |
 |
(73) |
 |
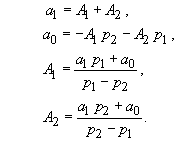(74) |
Die Partialbruchzerlegung lautet somit:
 |
(75) |
Beispiel: Gleichung (70), (71)