Kompendium > Diracimpuls

5.3 Faltungsalgebra (1)

In der Anwendung spielt der Diracimpuls eine große Rolle, besonders im Bereich der Berechnung von Fourier-Transformierten verschiedener Funktionen. In diesem Zusammenhang braucht man häufig auch die Faltung zwischen einer Funktion und dem Diracimpuls. Die Berechnung von Faltungsintegralen ist in der Regel aber mühsam, braucht jedoch in vielen Fällen gar nicht ausgeführt zu werden. Mit Hilfe der Darstellung als Faltungsprodukt kann man die Rechenoperation formal durchführen. Als Hilfsmittel kann man sich der folgenden Rechenoperationen bedienen.
Das Faltungsintegral ist definiert als:
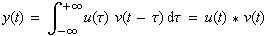(5-28)
In der Faltungsalgebra
  • gibt es ein Einselement:
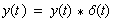(5-29)
  • gilt das Kommutativgesetz:
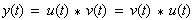(5-30)
  • und das Assoziativgesetz
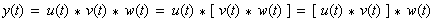(5-31)
Die Existenz des Einselementes kann man leicht mittels des Verschiebungssatzes zeigen. Kommutativ- und Assoziativgesetz lassen sich mit Hilfe von Substitutionen zeigen.