| Es sei eine Funktion |
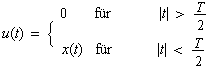
|
(4-1) |
| gegeben, deren Fourier-Transformierte U(ω)
ist. Durch Verschieben dieser Funktion jeweils um Vielfache der Periode
T kann man aus dieser Funktion eine periodische
Funktion konstruieren, wie es im Bild 4-1 gezeigt wird. |
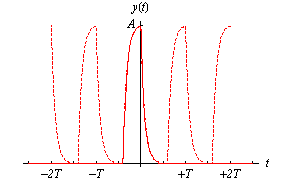
Bild 4-1 Periodische Funktion aus
einer Grundfunktion |
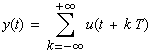
|
(4-2) |
| Die zugehörige Fourier-Reihe lautet mit |
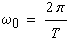
|
(4-3) |
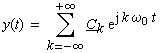
|
(4-4) |
| mit |
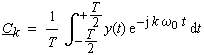
|
(4-5) |
| Setzt man anstelle der periodischen Funktion y(t)
die in der Grundperiode identische Funktion u(t)
ein, die aber außerhalb der Grundperiode identisch verschwindet, so
kann man die Grenzen des Integrals ausdehnen. |
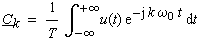
|
(4-6) |
| Man erhält also die Beziehung |
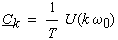
|
(4-7) |
| Dieses Ergebnis läßt sich so interpretieren: |
| Die Fourier-Transformierte ist bis auf den dimensionsbehafteten
Proportionalitätsfaktor 1/Τ
Hüllkurve für die Fourier-Koeffizienten der periodischen Funktion.
Für die Meßtechnik bedeutet dies, daß man das Spektrum
eines Einzelimpulses durch die Messung des Spektrums einer periodischen
Funktion aus diesen Einzelimpulsen ermitteln kann, wobei die Stützstellen
umso dichter liegen, je größer die Periode Τ
gewählt wird. |
