| Wie bei periodischen Funktionen läßt sich die Energie
wahlweise im Zeit- oder Frequenzbereich ermitteln. Mit der Umkehrtransformation
von y(t) findet man im Zeitbereich |
 |
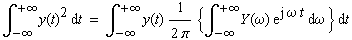(3-1) |
 |
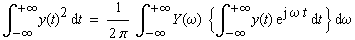(3-2) |
 |
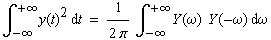(3-3) |
 |
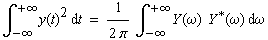(3-4) |
| Insgesamt erhält man das Parsevalsche Theorem: |
|
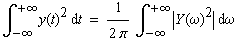
(3-5) |
| Die Energie des Signals kann man also im Zeitbereich (linke
Seite) oder im Frequenzbereich (rechte Seite) berechnen. |
| Zur Deutung der Parsevalschen Gleichung in der vorliegenden
Form kann man etwa folgenden Ablauf heranziehen: |
| y(t) sei ein Spannungsverlauf |
=> |
y(t)2 ist die Leistung |
|
=> |
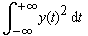 ist
die Energie |
|
=> |
|Y(ω)2| ist das Energiespektrum
oder die spektrale Dichte und dies identisch mit dem Quadrat der Amplitudendichte. |
|
