Kompendium > Diracimpumls |
|
| Mit sehr schmalen Impulsen lassen sich Einschwing- und Übertragungsverhalten von Systemen gut untersuchen. Für die theoretischen Betrachtungen ist es vorteilhaft, diese Impulse zu idealisieren. Man definiert einen unendlich schmalen Impuls mit der Impulsfläche 1, der aufgrund dieser Festlegung eine unendlich große Amplitude haben muß. Diese Funktion bezeichnet man als Diracimpuls. In der Praxis lassen sich Diracimpulse aus allen möglichen Impulsformen approximieren, z.B. Rechteck-, Dreieck-, cos2-Impuls usw. Der Diracimpuls tritt bei der Differentiation von Sprungstellen auf. Dazu betrachtet man die sogenannte Sprungfunktion σ(t) mit der Eigenschaft | |
| (5-1) | |
| siehe Bild 5-1. | |
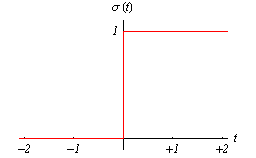 Bild 5-1 Darstellung eines idealisierten Einheitssprunges σ(t) |
|
| Dieser idealisierte Sprung tritt in der Praxis nicht auf, vielmehr gibt es nur Übergänge mit endlicher Flankensteilheit. Die Steigung Bild 5-2 beträgt 1/ 2 ε. Beim Differenzieren dieser Flanke entsteht ein Rechteckimpuls der Breite 2 ε und der Höhe 1/ 2 ε. Die sogenannte Impulsfäche Breite mal Höhe des Impulses beträgt eins. | |
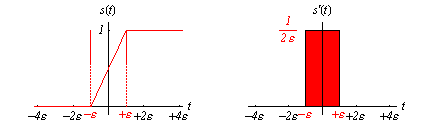 Bild 5-2 Darstellung eines realen Einheitssprunges σ(t) und dessen Ableitung |
|
| Läßt man ε nun immer kleiner werden, wird die Flankensteilheit der Funktion s(t) immer größer und gleichzeitig der Impuls immer schmaler und höher (siehe Animation). Die Impulsfläche bleibt aber konstant gleich eins. Im Grenzfall ε → 0 erhält man den Diracimpuls mit der Eigenschaft | |
| (5-2) | |
| und | |
| (5-3) | |
In der Analysis wäre eine solche Funktion nicht definiert. Die Theorie zur Untersuchung dieser speziellen Art von Funktionen findet man in der Distributionentheorie. Hier wird dieser Unterschied zwischen Distribution und Funktion durch die unterschiedliche Betrachtungsweise eines Einheitssprunges realisiert:
Es gilt |
|
| (5-4) | |