Kompendium > Kapazitive Vergleichsbrücke > Abgleich mit C2↔R2 (Bild 3)

Konvergenz des Abgleichs

Von einem Startwert xA, yA aus, wie oben als Messstrategie beschrieben, führt die wechselnde Einstellung von y bzw. x, jeweils bis zum lokalen Spannungsminimum, zum Abgleich mit x = 1, y = 1, p(1, 1) = 0.
Eine analoge Herangehensweise zur Betrachtung der Konvergenz des Abgleichs wie bei der Resonanzmessbrücke erfordert jedoch nun bei der Auswertung der Gleichung (31) Zeit, Motivation, Übersicht und Geschick bei den Vereinfachungen und den Lösungen der Nullstellengleichungen.
Es soll deshalb eine vereinfachende Betrachtung vorgenommen werden.
In der Nähe des Abgleichpunktes ist für den Wert der Diagonalspannung (Gleichung (12)) der Zählerterm von entscheidender Bedeutung, während der Nenner als konstanter Wert behandelt werden kann.
Der Zählerterm ist der Wert der Determinante
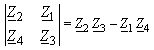(38)
und heißt Brückendeterminante ([Küpfmüller, 1933]).
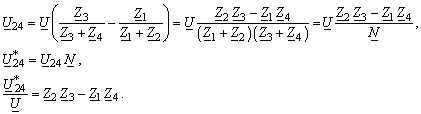(39)
Die Diagonalspannung verschwindet mit der Brückendeterminanten.
Den Gedanken umgesetzt auf die kapazitive Messbrücke (vgl. Gleichung (28)) erhält man
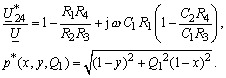(40)
Von einem Startwert in der Nähe des Abgleichs (z. B. 0,9 xA 1,1; 0,9 yA 1,1) sollen die Schritte bis zum Abgleich mit x = 1, y = 1, p(1, 1) = 0 betrachtet werden:
Beginnt man den Abgleich mit dem Wert yA und ändert x, ist zu untersuchen
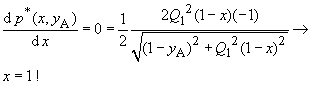(41)
Im nächsten Abgleichschritt folgt y = 1.
Beginnt man den Abgleich mit dem Wert xA und ändert y, ist zu untersuchen
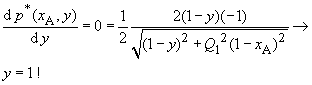(42)
Im nächsten Abgleichschritt folgt x = 1
Mit der Experimentierumgebung Kapazitive Messbrücke-Abgleich mit C2↔R2 und dem Mathcad-Arbeitsblatt MAB-Kapazitive Messbrücke können die aus der Bewertung der Gleichung (40) gewonnenen Ergebnisse zum Abgleichverhalten experimentell nachvollzogen werden.