Kompendium > Kapazitive Vergleichsbrücke > Abgleich mit C2↔R2 (Bild 3)
Kompendium > Kapazitive Vergleichsbrücke > Abgleich mit C2↔R2 (Bild 3) |
|
|
|
|
Als Abgleichempfindlichkeit im Abgleichpunkt soll folgender
Ausdruck bezeichnet werden: |
|
 |
(32) |
| in y-Richtung | |
 |
(33) |
| Setzt man als Näherung im Nenner von Gleichung (31) x = 1, y = 1, so folgt für obige Gleichungen: | |
 |
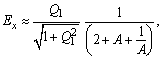(34) |
 |
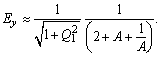(35) |
| Der Nennerterm in den Gleichungen (34), (35) | |
 |
(36) |
| ist minimal für A = 1. Für die Parametereinstellung |
|
 |
(37) |
| erhält man also maximale Abgleichempfindlichkeit im Abgleichpunkt. Diese Eigenschaft des sogenannten symmetrischen Brückenaufbaus (R3 = R4) kennen wir auch von der Wheatstoneschen Brücke und lässt sich auch bei der Resonanzmessbrücke zeigen. Mit der Experimentierumgebung Kapazitive Messbrücke-Abgleich mit C2↔R2 kann der Einfluss des Parameters A auf die Umrissdiagramme eindrucksvoll visualisiert werden. |
|
|