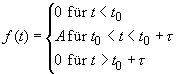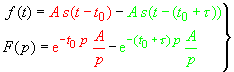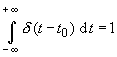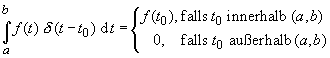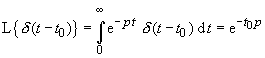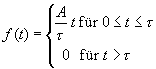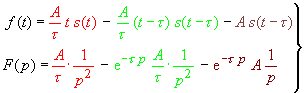Bildfunktionen ausgewählter Zeitfunktionen |
|
  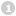     |
Bildfunktionen von Einzelimpulsen
Bildfunktionen von Zeitfunktionen, die nur in einem endlichen Zeitintervall
existent sind, lassen sich aus der Überlagerung zeitversetzter Grundfunktionen
rekonstruieren. Die Transformation der Einzelterme und die Anwendung des Additions-
und Verschiebungssatzes liefern die Bildfunktion des Einzelimpulses. Erkennt
man die Zerlegung nicht, hilft die Berechnung des Laplace-Integrals, wie in
den nachfolgenden Beispielen demonstriert wird.
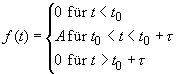 |
(43) |
Ein Rechteckimpuls lässt sich durch Überlagerung zweier zeitversetzter
Sprungfunktionen beschreiben:
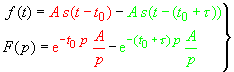 |
(44) |
Deltafunktion oder Diracfunktion
Die Deltafunktion δ(t
- t0)
ist anschaulich als Grenzfall eines Rechteckimpulses der Breite ε
und der Höhe 1 / ε
an der Stelle t0
interpretierbar:
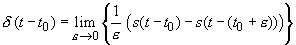 |
(45) |
Die Deltafunktion hat ihre Bedeutung (z.B. für netzwerkspezifische Anwendungen)
in der Multiplikation mit einer anderen Funktion unter einem Integral. Es ist
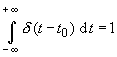 |
(46) |
Für eine stetige Funktion f(t)
gilt:
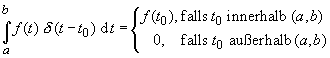 |
(47) |
Damit erhält man die Korrespondenz:
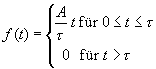 |
(51) |
Der Sägezahnimpuls lässt sich durch Überlagerung zeitversetzter
Grundfunktionen beschreiben:
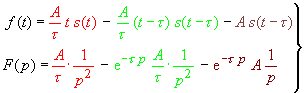 |
(52) |