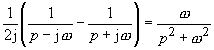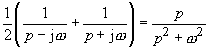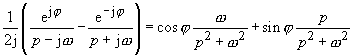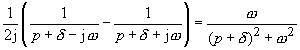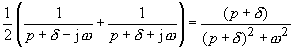Bildfunktionen ausgewählter Zeitfunktionen

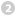Die grundlegenden Korrespondenzen

Sprungfunktion (Bild 1) (Herleitung)

Die Sprungfunktion s(t) vermittelt den Einheitssprung bei t = 0:

	(27)
	(28)
	(29)

Nach rechts verschobene Sprungfunktion (Bild 2)

(30)

Anwendung des Verschiebungssatzes für Verschieben nach rechts (t₀ > 0)

Exponentialfunktion (Bild 3) (Herleitung)

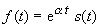(31)

Durch die Multiplikation der (Exponential-)Funktion mit der Sprungfunktion wird die Bedingung f(t) ≡ 0 für t < 0 realisiert.

(32)

Sinusfunktion (Bild 4) (Herleitung)

	(33)
	(34)

Kosinusfunktion

(35)

Sinusfunktion mit Nullphasenwinkel (Bild 5)

(36)

Gedämpfte Sinusfunktion (Bild 6)

(37)

vgl. auch Anwendung des Dämpfungssatzes

Gedämpfte Kosinusfunktion

(38)

vgl. auch Anwendung des Dämpfungssatzes

Rampenfunktion (Bild 7) (Herleitung)

	(39)
	(40)

Nach rechts verschobene Rampenfunktion (Bild 8)

(41)

Anwendung des Verschiebungssatzes (11)

Gedämpfte Rampenfunktion (Bild 9)

(42)

Anwendung des Dämpfungssatzes