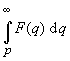Rechenregeln
Additions- oder Linearitätssatz
Verschiebungssatz für Verschiebung nach rechts
(Herleitung)
Die Laplace-Transformierte einer um t0
(t0
> 0) nach rechts verschobenen Originalfunktion f(t
- t0) mit f(t
- t0) ≡ 0
für t < t0
ist gleich der Laplace-Transformierten der nicht verschobenen Originalfunktion
f(t) ,
multipliziert mit dem Faktor e-t0
p.
Differenziationssatz im
Originalraum (Herleitung)
Analog folgt:
Integrationssatz im Originalraum (Herleitung)
Faltung im Originalraum (Herleitung)
Dabei wird als Faltung zweier Funktionen f1(t)
und f2(t)
das Integral
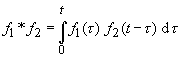 |
(19) |
bezeichnet.
Differenziationssatz im Bildraum (Multiplikationssatz)
(Herleitung)
Analog:
Integrationssatz im Bildraum (Divisionssatz) (Herleitung)
Falls 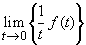 existiert
existiert
Grenzwertsatz für den Anfangswert (Herleitung)
Falls die Originalfunktion einen endlichen Grenzwert
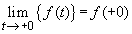 |
(23) |
besitzt, gilt:
 |
(24) |
Grenzwertsatz für den Endwert (Herleitung)
Falls die Originalfunktion einen endlichen Grenzwert
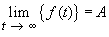 |
(25) |
besitzt, gilt:
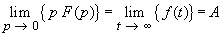 |
(26) |
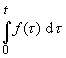
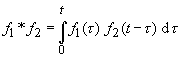
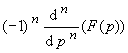
![]() existiert
existiert