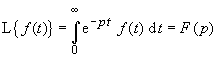Laplace-Transformierte, Original- und Bildraum (1)
Im Folgenden werden nur Funktionen f(t)
im Definitionsbereich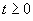 
betrachtet:
 . |
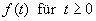(2) |
Das entspricht der Situation, dass häufig der Zeitverlauf f(t)
erst von einem bestimmten Zeitpunkt an gegeben ist oder interessiert (Einschaltvorgänge,
Abschaltvorgänge).
Die Laplace-Transformation
 |
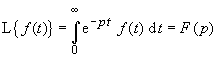(3) |
ordnet der gegebenen Originalfunktion f(t)
der reellen Veränderlichen t die Funktion F(p) der komplexen Veränderlichen p zu, die Bildfunktion
genannt wird.
Dabei gilt:
 , |
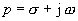(4) |
 . |
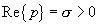(5) |
Der Dämpfungsfaktor e-σ t im Integral Gleichung (3) bewirkt, dass das Integral für möglichst
viele Originalfunktionen konvergiert.
Wenn f(t)
auf dem Intervall (0,∞) integrierbar ist
und die exponentielle Wachstumsbeschränkung
 |
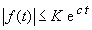(6) |
erfüllt, dann konvergiert das Integral Gleichung (3) für Re{p}
= σ > 0 .
