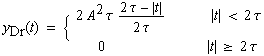Beispiel 4 (3) |
| Mit Hilfe des Faltungssatzes läßt sich die Fourier-Transformierte
des Dreieckimpulses aus der Faltung von Rechteckimpulsen berechnen: |
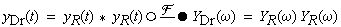 |
(B4-2) |
| Aufgrund dieser Darstellung des Dreieckimpulses als Faltung
von Rechteckimpulsen ergibt sich zusammen mit der Fourier-Transformierten
des Rechteckimpulses - siehe Beispiel B1
- die Fourier-Transformierte des Dreieckimpulses aus dem Produkt der Fourier-Transformierten
der Rechteckimpulse |
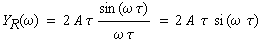 |
(B4-3) |
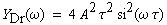 |
(B4-4) |
| Die Größe (2 A
τ)2 stellt dabei wieder die Impulsfläche
des Dreieckimpulses dar. |
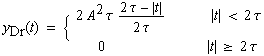 |
(B-5) |
| Es läßt sich aus dieser Impulsform wieder der
Diracimpuls δ(t) gewinnen, wenn bei
konstanter Impulsfläche |
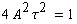 |
(B4-6) |
| die Breite des Impulses gegen Null strebt. |
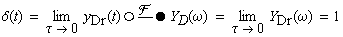 |
(B4-7) |