Beispiele > Beispiel 2
Beispiele > Beispiel 2 |
|
|
|
| Im Bild B2-2 ist das Spektrum abgebildet. Um in der Zeichnung den Schnittpunkt mit der Ordinate zu erhalten, muß die Fourier-Transformierte für ω → 0 betrachtet werden. Man erhält unter Anwendung des Satzes von Bernoulli L'Hospital | |
 |
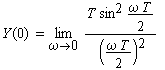(B2-9) |
 |
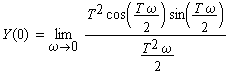(B2-10) |
 |
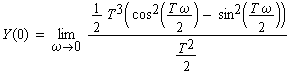(B2-11) |
 |
(B2-12) |
| Berührungspunkte mit der ω-Achse Y(ω) = 0 ergeben sich für: | |
 |
(B2-13) |
|
|
| Man erkennt harmonische Schwingungen aller Frequenzen sind am Aufbau des Dreieckimpulses beteiligt. Es überwiegen die Frequenzen | |
 |
(B2-14) |
| bzw. | |
 |
(B2-15) |
| d.h. es würde in diesem Fall in erster Näherung auch genügen, das Integral im Intervall | |
 |
(B2-16) |
| für ω und im Intervall | |
 |
(B2-17) |
| für f zu betrachten (siehe Animation 1). Ebenso erkennt man, daß zu einem Signal von kurzer Dauer ( d.h. τ klein und damit y(t) in einem kleinen Intervall ungleich 0 ) ein breiteres Frequenzband gehört (f = n/Τ mit Τ → 0 => f → ∞ bzw. die Spektralfunktion Y(f) ist in einem großen Intervall ungleich 0 ) (siehe Animation 2). | |
