Bestimmung der Fourier-Koeffizienten für symmetrische
Funktionen
Die Bestimmung der Fourier-Koeffizienten an
und bn aus den
Gleichungen (13),
(14)
vereinfacht sich, wenn zu den Symmetrieeigenschaften
der Sinus- und Kosinuszeitfunktionen auch Symmetrieeigenschaften
der Funktion f(t)
vorliegen.
Eine achsensymmetrische (gerade) Funktion hat die Eigenschaft
f(t)
= f(-t)
(Beispiel: Rechteckimpulsfolge).
Eine nullpunktsymmetrische (ungerade) Funktion hat die Eigenschaft f(t)
= -f(-t)
(Beispiel: Sägezahnfunktion).
Eine Halbwellensymmetrie 1. Art liegt vor für f(t
+ T/2) = -f(t)
(Beispiel: Rechteckfunktion).
Die Halbwellensymmetrie 2. Art liegt vor für f(t
+ T/2) = f(t).
Eine Funktion als Produkt zweier Funktionen mit Symmetrieeigenschaften
(z. B.: g(t)
= f(t)
cos(nω
t), g(t)
= f(t)
sin(nω
t) hat wieder Symmetrieeigenschaften
Symmetrieeigenschaften
von Produkten symmetrischer Funktionen).
Integrale
von Funktionen mit Symmetrieeigenschaften berechnen sich vereinfacht.
Für eine achsensymmetrische Funktion f(t)
vereinfachen sich die Gleichungen (13),
(14),
(18)
zur Berechnung der Fourier-Koeffizienten:
|
|
 |
(29) |
| Für eine nullpunktsymmetrische Funktion f(t)
erhält man die Fourier-Koeffizienten: |
|
 |
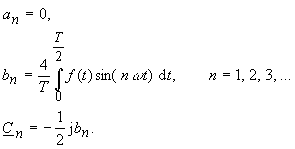(30) |
| Hat die Funktion die Eigenschaft der Halbwellensymmetrie (1. Art) folgt:
|
|
 |
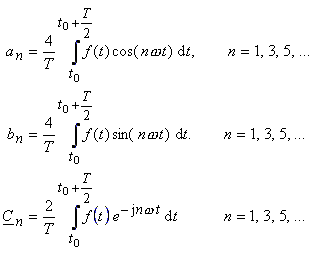(31) |
Im Spektrum fehlen die geradzahligen Harmonischen.
Ist die Funktion f(t)
achsensymmetrisch und halbwellensymmetrisch (1. Art) (Beispiel: Rechteckfunktion
2), gilt: |
|
 |
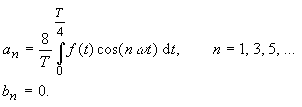(32) |
| Ist die Funktion f(t)
nullpunktsymmetrisch und halbwellensymmetrisch (1. Art) (Beispiel: Rechteckfunktion
1), gilt: |
|
 |
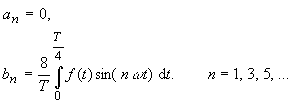(33) |
Zur Visualisierung obiger Sachverhalte können die Integranden
in den Gleichungen (13),
(14)
für verschiedene Signalfunktionen und unterschiedliche n
dargestellt werden.
|
|
  |
|
