Kompendium |
|
| Komplexe Fourier-Reihe | |
Eine gleichwertige Darstellung der Fourier-Reihe Gleichung (15) ist der Ansatz |
|
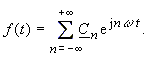 |
(16) |
| Mit den Zerlegungen über die Eulersche Formel | |
|
|
| erhält man für die Gleichung | |
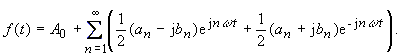 |
(17) |
| Gleichfrequente Cosinus- und Sinusglieder lassen sich durch ein konjugiert
komplexes Zeigerpaar mit entgegengerichtetem Drehsinn darstellen. Der Vergleich der Ansätze (16) und (17) liefert den Zusammenhang: |
|
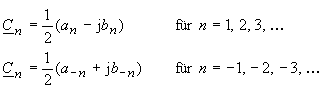 |
(18) |
| Setzt man nun die Gleichungen (13) und (14) in Gleichung (18) ein, folgt die Berechnungsvorschrift für den Koeffizienten Cn: | |
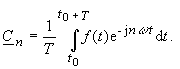 |
(19) |
| Für n = 0 geht Gleichung (19) in Gleichung (10) über: | |
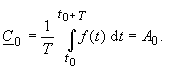 |
(20) |
| Diese komplexe Darstellung hebt die Ausnahmestellung des Konstantgliedes A0 auf, das nunmehr zwischen die positiven und negativen n-Werte eingefügt wird, und reduziert den Aufwand auf die Berechnung des Fourier-Koeffizienten Cn . Diese Darstellung ist auch nützlich bei der Weiterentwicklung der Fourier-Reihen-Betrachtungen zur Fourier-Transformation sowie bei systemtheoretischen Betrachtungen. | |