Kompendium
Einführung

Spektrale Darstellungen

 

  
Die Fourier-Reihe nach Gleichung (15) lässt sich durch Zusammenfassen der gleichfrequenten Cosinus- und Sinusglieder gleichwertig wie folgt darstellen:  
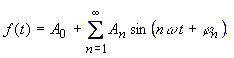(21)
Wegen  
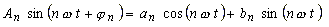(22)
rechnet man mittels komplexer Rechnung die kartesischen Koordinaten bn, an des Bildpunktes in die Polarkoordinaten An , φ n um:  
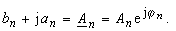(23)
Für die Amplitude An gilt  
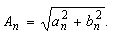(24)
Für den Nullphasenwinkel j n erhält man z. B. mit an > 0, bn > 0 (1. Quadrant)  
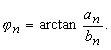(25)
Für Bildpunkte auf den Achsen bzw. im 2., 3., und 4. Quadranten rechnet man den Winkel entsprechend um.

Bildpunkte
Das Amplitudenspektrum ist nun die Darstellung der Werte An über n (0 ≤ n < ∞ ) und damit ein diskretes Linienspektrum.
Das Phasenspektrum ist die Darstellung der Werte φn (in Grad oder Bogenmaß) über 1 ≤ n < ∞ und damit ebenfalls ein diskretes Linienspektrum.
Die Werte werden für die Darstellung auf das Intervall -180° < φn ≤ +180° bzw. -π < φn ≤+π umgerechnet. Im Bild sind die Spektren für eine um tL verschobene Rechteckfunktion (vgl. Beispiel 3) angegeben.
Die komplexe Darstellung der Fourier-Reihe (Gleichung (16)) mit dem Fourier-Koeffizienten Cn liefert eine gleichwertige Spektraldarstellung für die Funktion f(t).
Mit

 
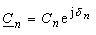(26)
werden nun die Cn, δn über - ∞ < n < +∞ aufgetragen.
Da nun jede Harmonische durch einen Zeiger und den konjugiert komplexen Zeiger repräsentiert wird (z. B. n = 3, C3, C-3, Gleichung (18)), ist das Amplitudenspektrum Cn achsensymmetrisch und das Phasenspektrum δn nullpunktsymmetrisch, so dass die Darstellung über 0 ≤ n < ∞ ausreicht.
Für die Umrechnung der Spektren folgt aus den Gleichungen (18), (23) 		 
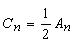(27)
und wegen (n > 0)  

 

 (28)
beispiel 3  
Einführung