Kompendium |
|
Ermittlung der Fourier-Koeffizienten Nach welchen Gesichtspunkten sollen die Koeffizienten
A0, an,
bn gewählt werden? |
|
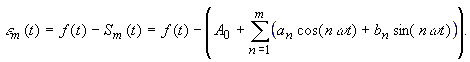 |
(4) |
| Nach Gauss macht man den mittleren quadratischen Fehler M | |
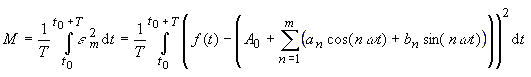 |
(5) |
| durch Wahl der A0, an,
bn zu einem Minimum. Diese Forderung führt zu den Gleichungen: |
|
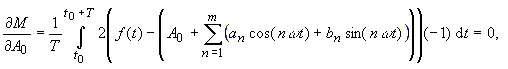 |
(6) |
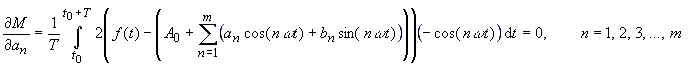 |
(7) |
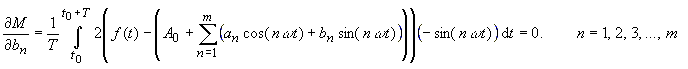 |
(8) |
| Da nun aber | |
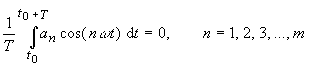 |
|
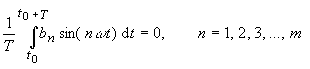 |
|
| folgt | |
|
(9) |
| und damit aus Gleichung (6) | |
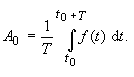 |
(10) |
| Das Konstantglied A0 in der Fourier-Reihe
ist, wie erwartet, der arithmetische Mittelwert, der Gleichanteil (Gleichwert)
der Funktion f(t)! Die Berechnungsvorschriften der Koeffizienten an, bn (Gleichungen (7), (8)) vereinfachen sich. Diese Aussage folgt aus der Eigenschaft der Orthogonalität der trigonometrischen Funktionen auf dem Intervall Es ist nämlich |
|
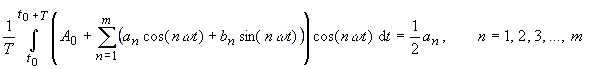 |
(11) |
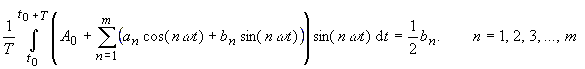 |
(12) |
| Damit erhält man aus den Gleichungen (7) und (11) | |
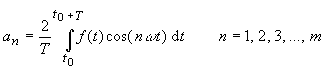 |
(13) |
| und aus den Gleichungen (8) und (12) | |
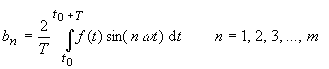 |
(14) |
| Das Bemerkenswerte ist, dass offenbar jeder Koeffizient A0,
an, bn
für sich direkt aus den Gleichungen (10),
(13), (14) bestimmbar
ist. Die Koeffizientenberechnung ist nicht miteinander verknüpft. Approximiert man z. B. die Funktion f(t) durch die Reihe |
|
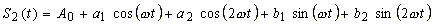 |
|
| und bestimmt die Koeffizienten A0,
a1, a2,
b1, b2
aus den Gleichungen (10),
(13), (14)
und verbessert nun die Approximation durch Hinzunahme der Glieder |
|
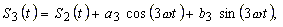 |
|
| so bleiben die Koeffizienten A0,
a1, a2,
b1, b2
unverändert. Eine zweite herausragende Eigenschaft ist: Wenn die Funktion f(t) im Intervall [t0, t0+T] bestimmte von Dirichlet aufgestellte Bedingungen einhält, dann konvergieren für m → ∞ die Funktionswerte der nun unendlichen Fourier-Reihe gegen die Funktionswerte f(t) |
|
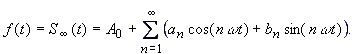 |
(15) |
Das ist eine überraschende Aussage: |
|