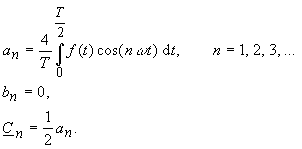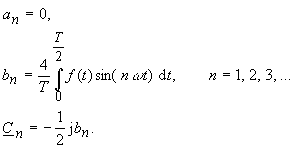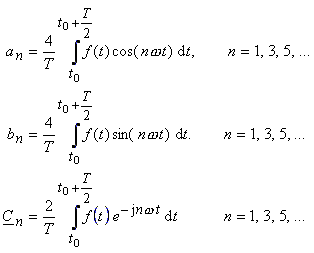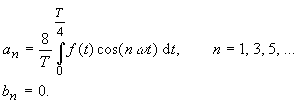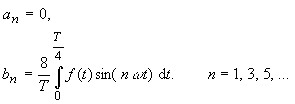determination of the Fourier Coefficients for symmetric
functions
The determination of the Fourier-coefficients an
und bn from
the equations (13),
(14)
is much simpler if the symmetriy
properties are not only known for the sine- and cosine-timefunctions
but also for the function f(t).
An axially symmetrical (even) function has the characteristic f(t)
= f(-t)
(for example :rectangular
pulse train).
A (uneven) function symmetrical to the origin has the characteristic f(t)
= -f(-t)
(for example:saw-tooth
function).
A half wave symmetry of the first kind exsists for f(t
+ T/2) = -f(t)
(for example: rectangular-function)
A function as the product of two functions with symmetry property
(e.g. g(t) = f(t) cos(nω
t), g(t) = f(t)
sin(nω
t) has symmetry property too.
(symmetry properties of products of symmetric functions).
Integrals of functions with symmetry properties can be calculated
easily:
For an axially symmetrical function f(t)
the equations (13),
(14),
(18)
for the calculation of the Fourier coeficiens simlify :
|
|
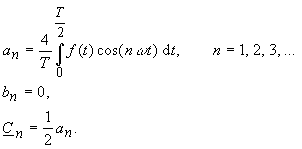 |
(29) |
| For a function f(t)
symmetric to the origin one obtains the Fourier coefficient: |
|
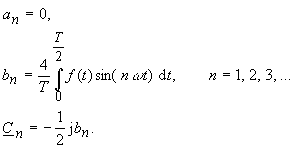 |
(30) |
If the function is half wave symmetrical (1st kind) it follows:
|
|
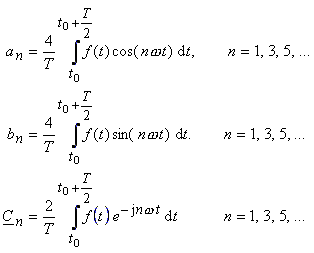 |
(31) |
The even numbered harmonics are missing in the spectrum.
If the function f(t)
is axially symmetrical and half wave symmetrical (1st kind) (e.g.: rectangular
function ), it applies : |
|
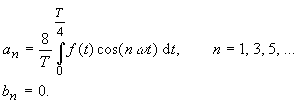 |
(32) |
| If the function f(t)
is symmetrical to the origin and half wave symmetrical (1st kind) (e.g. rectangular
function it applies: |
|
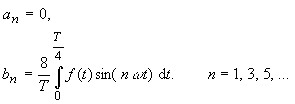 |
(33) |
To visualize the circumstances above the integrands of the equations
(13),
(14)
can be displayed for various signal functions and different n.


|
|