compendium |
|
Fourier-SeriesA periodic function |
|
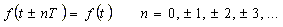 |
(1) |
| is to be approximated by the sum of 2m trigonometrical elements and a constant element on the interval of [t0, t0+T ] (finite Fourier-Series): | |
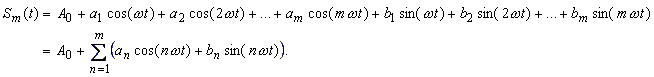 |
(2) |
| The coefficients A0,
a1,
a2,
..., am,
b1,
b2,
..., bm
are the so called Fourier-coefficients. The coefficient A0 in equation (2) is to be expected as the constant component (equivalent value) of the function f(t). ω is the angular frequency of the fundamental wave and accordingly of the 1st harmonic. nω (n = 2, 3, 4, ..., m) are the angular frequencies of the overtones and accordingly of the 2nd., 3rd., 4th. , …, n-th harmonic. The angular frequency of the fundamental wave ω and the period duration T of the function f(t) are in coherence: |
|
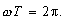 |
(3) |