compendium |
|
| complex Fourier-Series | |
A equivalent representation of the Fourier Series (equation 15) is the approach |
|
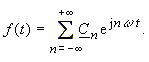 |
(16) |
| of the decomposition using Euler's formula | |
|
|
| one obtains for the equation | |
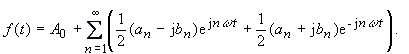 |
(17) |
| Cosine- and sine elements with the same frequency can be represented by
a conjugated pair of phasors with an opposite direction of rotation. The comparison of the approach (16) to (17) provides the coherency: |
|
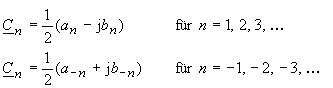 |
(18) |
| If the equations (13) and (14) are put into the equation (18) we obtain the algorithm for the coefficient Cn: | |
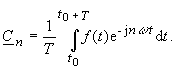 |
(19) |
| For n = 0 the equation (19) merges into the equation (10) : | |
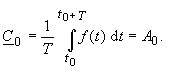 |
(20) |
| This complex equation stresses the special position of the constant element
A0. whitch is from now on inserted
between the positive and the negative n-values
and simplifies the calculation of the Fourier-coefficient Cn.
This representation is very usefull for the enhancement of the treatment
of Fourier series to the Fourier transformation or for system theoretical
approaches. |