compendium
Einführung

calculation of the Fourier-Coefficients

So how should the coefficients A0, an, bn be chosen?
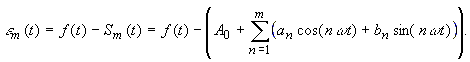For every point in time t there is an error

  
(4)
According to Gauss you can minimize the average quadratic error M  
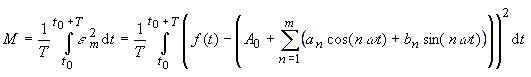(5)
by choosing A0, an, bn
This claim leads to the equations:		  
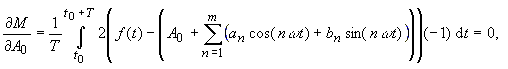(6)
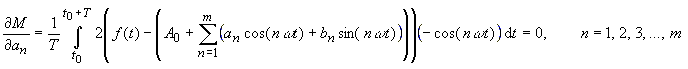(7)
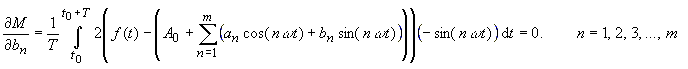(8)
but since  
 
 
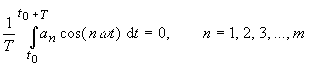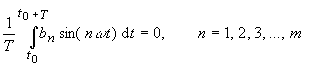it follows  
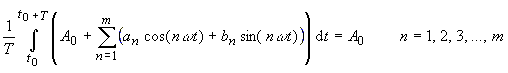(9)
and for that reason from equation (6)  
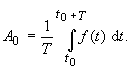(10)
The constant element A0 of the Fourier-series is (as expected) the arithmetic average, the constant component (the average value) of the function f(t)!
The algorithm for the coefficientsan, bn (equations (7), (8)) becomes simpler . This statement follows from the property of orthogonality of trigonometric functions on the interval of [ t0, t0+T ].
Thus it is:		  
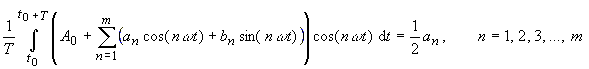(11)
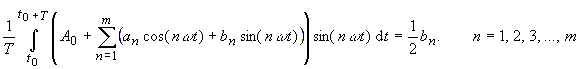(12)
with this one obtains from the equations (7) and (11)  
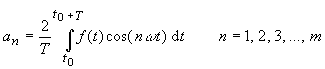(13)
and from the equations (8) and (12)  
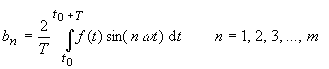(14)
Apparently every coefficient A0, an, bn is estimable itself directly from the equations (10), (13), (14). The calculation of the coefficients is not linked with each other.
For example: if one approximates the function f(t) using the series
  
 
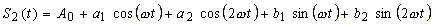and determines A0, a1, a2, b1, b2 from the equations (10), (13), (14) and now improves the approximation by adding the elements a3cos(3nωt), b3sin(3 nωt)  
 
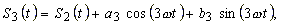the coefficients A0, a1, a2, b1, b2 stay unchanged.
Another remarable feature is: If the function f(t) on the interval of [t0, t0+T] adheres to certain requirements purposed by Dirichlet , the values of function of this infinite fourier series (for m → ∞) approach the values of function f(t).		  
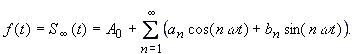(15)

This is a suprising statement:
The periodic functions we are dealing with here are commonly discontinuous lines. Thus they can be represented by superimposing a series of simple coninous functions.

  

beispiel 1

Einführung