compendium
Einführung

spectral representations

 

  
The Fourier series according to equation (15) can be represented equally by combining the cosine and sine elements of the same frequency:  
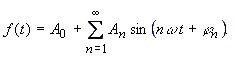(21)
because of  
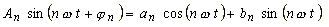(22)
the Cartesian coordinates bn, an of the image element are converted to the polar coordinates An , φ n using a complex arithmetic:  
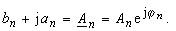(23)
For every amplitude An it is essential that:  
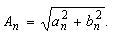(24)
For the phase lead/lag j n we obtain (for example for an > 0, bn > 0 (1st . quadrant) )  
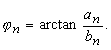(25)
The angles of the image elements on the axis or respectively inside the 2nd, 3rd and 4th quadrant are converted accordingly.

image elements
The amplitude spectrum now is the representation of the values An (for n from 0 to ∞). For that reason is a discrete line spectrum.
The phase spectrum is the representation of the values φn (in circular measure or degree) across 1 ≤ n < ∞ and for that reson it is a descrete line spectrum too.
For the representation the values have to be converted to the interval -180° < φn ≤ +180° or -π < φn ≤+π. In the image we can see the spectras for a rectangular function shifted by tL Im (compare to example 3).
The complex representation of the Fourier-series (equation(16)) with the Fourier-coefficient Cn provides us with an equivalent spectral representation of the function f(t).
Using

  
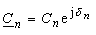(26)
the Cn, δ n are added up across - ∞ < n < +∞ .
Every harmonic is represented by a phasor and the conjugated comlex phasor (e.g. n = 3, C3, C-3, equation(18)) That is why the amplitude spectrum Cn is axially symmetrical and the phase spectrum δ n is symmetrical to the origin. On account of this the representation acrosss 0 ≤ n < ∞ is sufficient.
For the conversion of the spectras it follows from the equations (18), (23) : 		 
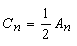(27)
and because of (n > 0)  

beispiel 3

 (28)

Einführung