Kompendium > Resonanzmessbrücke > Abgleich mit f↔R2 (Bild 2)

Zweischrittabgleich, Dreischrittabgleich

Die Auswertung der Gleichung (20) liefert auch Aussagen zur Konvergenz des Brückenabgleichs. Die Erwartung ist, dass von einem Startwert xA, yA aus die wechselnde Einstellung von y bzw x, jeweils bis zum lokalen Spannungsminimum, letztlich zum Abgleich mit x = 1, y = 1, p(1,1)=0 führt.
Wie aus der Vorgehensweise bei Kurvendiskussionen bekannt, erhält man die Stelle der lokalen Minima aus Extremwertbetrachtungen:
Beginnt man den Abgleich mit einem beliebigen Wert R2, (yA) und ändert die Frequenz f, (x), ist zu untersuchen
(21)
Mit der Quotientenregel folgt:
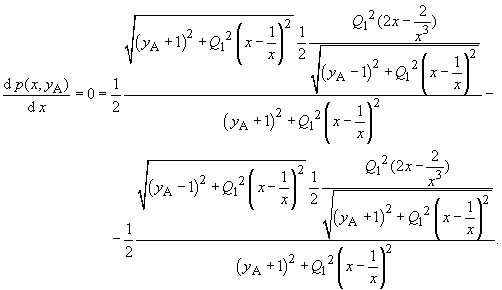(22)
Diese „furchterregende“ Nullstellengleichung (22) vereinfacht sich schnell, wenn man mit dem Term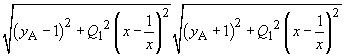 durchmultipliziert.
Der Zähler ist null für x = 1!
Der dazu gehörige Spannungswert (lokales Minimum) ist p(1,yA).
Beginnt man also den Abgleich mit einem beliebigen Wert R2, (yA), führt die Frequenzänderung bis zum lokalen Minimum sofort zur Komponente des Abgleichs f = f0, (x = 1)
Im zweiten Schritt wird mit R2 = R1, (y = 1) der Abgleich U24 = 0, p(1,1) = 0 erzielt (Zweischrittabgleich).
Beginnt man bei einer beliebigen Frequenz f, (xA) mit der Variation von R2, (y),ist
(23)
zu untersuchen.
Die ganz analoge Vorgehensweise, wie oben demonstriert, liefert für den y-Wert des lokalen Minimums der Diagonalspannung
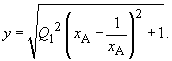(24)
Nun wird im zweiten Schritt die Frequenz f auf die Resonanzfrequenz f0, (x = 1) des Reihenresonanzkreises abgestimmt.
Im dritten Schritt ist mit R2 = R1, (y = 1) der Abgleich U24 = 0, p(1,1) = 0 erzielt (Dreischrittabgleich).

Mit der Experimentierumgebung Resonanzmessbrücke können durch Auswertung der Umrissdiagramme und Nutzung der Abgleich-Optionen die aus der Bewertung der Gleichung (20) gewonnenen Ergebnisse zum Abgleichverhalten experimentell nachvollzogen werden.
Die Ergebnisse zur Konvergenz des Brückenabgleichs sind im Mathcad-Arbeitsblatt MAB-Resonanzmessbrücke dargestellt.