2.5 Bedeutung der Elemente im T-Ersatzschaltbild

für einen symmetrisch aufgebauten Transformator
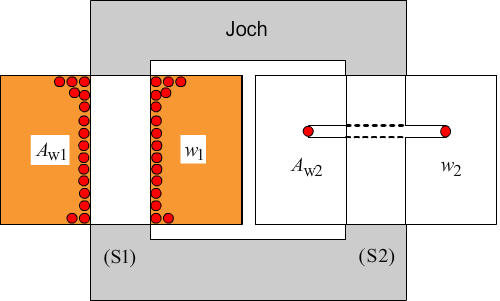
Im Abschnitt 2.1 ist für den Einphasenkern-Transformator gesagt worden, dass auf die Schenkel 1 und 2 die Wicklungskörper aufgeschoben werden und danach wird der Eisenkreis durch Anbringen der Joche geschlossen. Bei kleineren Transformatoren sind es Pertinax-Spulenkörper, die die Wicklungen tragen und deren Inneres anschließend durch geschichtete Eisenbleche (UI-, L-, EI- bzw. M-Schnitte) zu einem geschlossenen Eisenkreis (in der Regel ohne Luftspalt) ausgefüllt werden. Das innere Fenster des Eisenkörpers lässt also nur einen bestimmten Wickelraum Aw für die Primär- und Sekundärwicklung (Bild 8) zu.
Beim symmetrisch aufgebauten Transformator sind die Wickelfensterquerschnitte Aw1 = Aw2 = Aw gleich groß.
Bild 8: Spulenkörper mit Primär- und Sekundärwicklung und angedeuteter mittlerer Drahtlänge in der Wicklung 2
Der Leitungswiderstand R1 der Wicklung 1 berechnet sich aus:
2.5-(1)
mit
2.5-(1.1)
lges1: gesamte Drahtlänge
lm  : mittlere Drahtlänge einer Windung
ADr1: Drahtquerschnitt
In dem Wickelfenster lässt sich nur ein bestimmter Drahtquerschnitt ADr1 bei vorgegebenem Primärstrom I1 entsprechend der zulässigen Stromdichte
und damit eine bestimmte Drahtlänge unterbringen. Bezieht man das Wickelfenster Aw ein, so gilt
mit
2.5-(1.2)
kCu1 ist der sogenannte Kupferfüllfaktor, der angibt, wie dicht das Wickelfenster 1 mit dem Kupferdraht ausgefüllt ist.
Damit erhält man für den Wicklungswiderstand R1
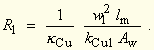2.5-(2)
Analog lässt sich für den Widerstand R'2 = ü2 R2 angeben:
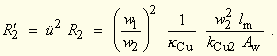2.5-(3)
wenn ebenso
2.5-(3.1)
eingeführt wird. Unter der Annahme, dass kCu1 ≈ kCu2 ist, folgt aus dem Vergleich von R1 mit R'2
2.5-(4)
Wir halten fest:
Bei einem symmetrisch aufgebauten Transformator ist: R1 = R'2 .
Die Definitionsgleichungen für die Induktivitäten L1 und L2 sind (Reihenfolge der Indizes: 1. Index – Ort der Verkettung; 2. Index – verursachender Strom):
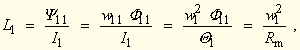2.5-(5)
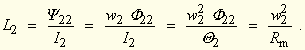2.5-(6)
Aus Sicht der jeweiligen elektrischen Erregungen oder (magnetische Quellen) ist der magnetische Widerstand Rm für den Einphasentransformator gleich groß.
Die Gegeninduktivität M = L12 = L21 (gegenseitige Induktivität) erhält man aus L1 und L2 über
2.5-(7)
mit dem Koppelfaktor k. Damit wird aus üM mit den Gleichungen 2.5-(5) und 2.5-(6):
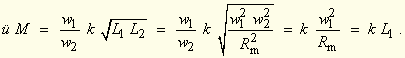2.5-(8)
Die transformierte Gegeninduktivität üM = kL1 = Lh (Lh: Hauptinduktivität) steht für den magnetischen Hauptfluss Φh = Φ12 = Φ21, der im Eisenkreis beide Wicklungen vollständig durchsetzt
Mit den vorangegangenen Ergebnissen lässt sich nun auch L1 – üM leicht als primäre Streuinduktivität Lσ1
2.5-(9)
deuten, die für den Streufluss der Wicklung 1 steht. Wir bezeichnen ü2L2 – üM = L'σ2 als die reduzierte sekundäre Streuinduktivität und gewinnen sofort die wichtige Beziehung
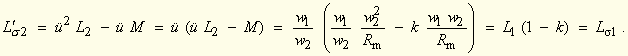2.5-(10)
Für einen symmetrisch aufgebauten Transformator ist: .
2.5-(11)
Bleibt die berechtigte Frage, warum gesetzt wurde. Der Koppelfaktor k ist das geometrische Mittel aus den einzelnen Koppelfaktoren k21 = (1 – σ1) und k12 = (1 – σ2), und diese sind das Komplement zu den jeweiligen Streufaktoren σ1 und σ2:
2.5-(12)
Setzen wir σ1 + σ2 = σ und vernachlässigen das Produkt σ1σ2 wegen σ1 << 1 bzw. σ2 << 1, so ergibt sich aus der Reihenentwicklung der Wurzelfunktion
bzw.
2.5-(12.1)
Die im Ersatzschaltbild (Bild 7) aus den mathematischen Umformungen folgenden Längsinduktivitäten haben damit eine physikalische Bedeutung erhalten. Sie wurden als primäre und sekundäre Streuinduktivitäten gedeutet, die für die primären und sekundären Streuflüsse der beiden Wicklungen stehen:
bzw.
2.5-(13)
wenn jeweils nur die primäre Erregung bzw. nur die sekundäre Erregung allein wirksam ist.