Kompendium

Klirrfaktor und Grundschwingungsgehalt

Während Effektivwert und Wirkleistung für Mischgrößen (Gleichanteil und Wechselanteil) angegeben werden, bezieht sich die Klirrfaktorangabe auf (reine) Wechselgrößen.
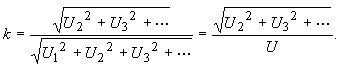Der Klirrfaktor ist ein Maß für die Abweichung einer nichtsinusförmigen periodischen Zeitfunktion vom sinusförmigen Verlauf. Der Name bezieht sich auf die typischen Verzerrungsgeräusche in der Tonstudiotechnik und im HiFi-Bereich.
Hat man z. B. eine nichtsinusförmige Spannung mittels Fourier-Analyse in eine Summe von Harmonischen zerlegt, so ist der Klirrfaktor per Definition der Quotient aus dem Effektivwert der Oberwellen zum Effektivwert der Gesamtspannung:

  
(42)
Oft wird auch der prozentuale Klirrfaktor k% angegeben:  


                  k% = k ·100 %

  
Als Klirrfaktor für die n-te Harmonische bezeichnet man:  
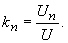(43)
Eine geeignete Möglichkeit ist, den Klirrfaktor aus dem Grundschwingungsgehalt g zu berechnen. Der Grundschwingungsgehalt g ist der Klirrkoeffizient der 1. Harmonischen (Grundwelle):  
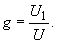(44)
Aus den Gleichungen (42) und (44) folgt nämlich:  
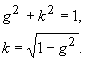(45)
Betragsgleiche Klirrfaktoren können trotz gleicher Grundwellenfrequenz verschieden im Schaubild aussehen und verschieden klingen, da sie auf verschiedenen Oberwellen beruhen können (Experimentierumgebung Klirrfaktor). Der Gesamtklirrfaktor hintereinander geschalteter Baugruppen a, b, c, ... wird wie folgt angegeben:  
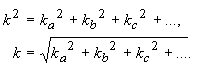(46)

Anwendung findet die Klirrfaktorangabe unter anderem

  • in der quantitativen Beschreibung sogenannter linearer und nichtlinearer Verzerrungen,
  • in der Tonstudio- und HiFi-Technik als "Qualitätsangabe" für Audiokomponenten,
  • in der Beschreibung von Systemen mit Filtereigenschaften
    		•   
    Beispiel 7 Beispiel 8