2.9.2 Arbeitshypothesen und Versuch ihrer Verifizierung
Kompendium
Die aufgenommenen Hystereseschleifen sind der summarische Ausdruck der Überlagerung des nichtsinusförmigen Leerlaufstromes i1l(t) (bzw. der zugehörigen Feldstärke H(t) ) und des dazu um 90° phasenverschobenen sinusförmigen Flusses Φh(t) (bzw. der Induktion B(t) ). Die Hystereseschleife widerspiegelt in jedem Fall sowohl das Auftreten
  • der Hystereseverluste PH beim einmaligen Durchlaufen der Hystereseschleife als ein Bestandteil der Eisenverluste PFe
2.9-(6)
aber auch noch
  • die Wirbelstromverluste PWb in den einzelnen Blechen des Eisenpaktes (bzw. im Stahlstück) als ihrem zweiten wichtigen Bestandteil.
Die Eisenverluste (oder auch Ummagnetisierungsverluste genannt) sind im Versuch GET14 „Messung der Eisenverluste“ genauer beschrieben, so dass an dieser Stelle auf die dortigen Ergebnisse zurückgegriffen wird.
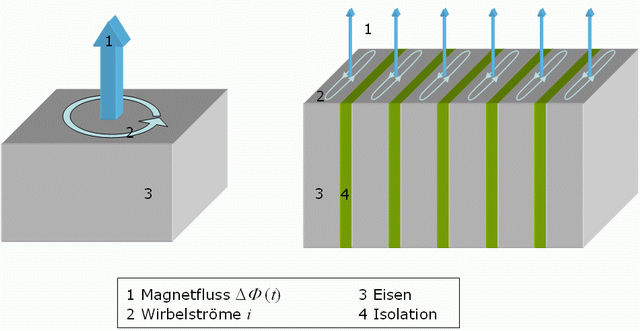
Die Wirbelströme stellen eine räumliche elektrische Strömung in den einzelnen zueinander isolierten Blechen des Eisenpaketes dar, die durch die in den Blechen vorhandenen Flussanteile ΔΦ(t) des homogen verteilten Hauptflusses Φh(t) auf Grund des Induktionsgesetzes wirksam werden.
Bild 15: Wirbelstrombahnen in einem Eisenstück und den Einzelblechen eines Blechpaketes
 
Ihre analytische Behandlung unter vereinfachenden Annahmen liefert in einem Eisenblech die Wirbelstromverluste PWb (siehe Versuch GET14):
2.9-(7)
κFe : elektrische Leitfähigkeit des Blechmaterials
a, l   : Blechabmessungen
d      : Blechdicke eines Einzelbleches
 
Die Formeln für die Hysterese- und Wirbelstromverluste wurden hier in erster Linie angegeben, um ihre funktionellen Abhängigkeiten von
  • der Kreisfrequenz ω bzw. der Frequenz f ,
  • der Induktion und
  • der Blechdicke d
hervorzuheben.
 
Die Gleichung für die Wirbelstromverluste in einem Einzelblech gilt nur unter der Annahme, dass keine Rückwirkung der Wirbelströme auf das erregende B-Feld angenommen wird. Diese Annahme ist für

Frequenzen f < 100 Hz,

Blechdicken d < 1 mm
sicher erfüllt, wie es die Ergebnisse des Versuches GET14 zeigen. Für den Transformatorkern mit dem massiven Stahlstück der Dicke d = 15 mm ist allerdings davon auszugehen, dass das magnetische Eigenfeld der Wirbelströme zur Flussverdrängung des Erregerfeldes aus dem Inneren des Stahlstückes auf eine Randzone und damit zur Feldunsymmetrie führt. Unser Transformatormodell basiert aber auf der Homogenität der Fluss- bzw. Induktionsverteilung im Eisenkern; insbesondere ist die Transformatorformel unter dieser Maßgabe (direkte Proportionalität von magnetischer Induktion und angelegter Spannung U) hergeleitet worden. Die Messergebnisse für die Effektivwerte der Primärspannung U1 = Ueff werden zeigen, dass diese Proportionalität aufgehoben und eine höhere Spannung zur Induktionseinstellung gegenüber dem theoretisch errechneten Wert notwendig ist.
 
Wir wollen nun eine Arbeitshypothese formulieren:
 
Die Hystereseschleife widerspiegelt in ihrem Verlauf die gesamten Eisenverluste
2.9-(8)
und sollte deshalb besser „Ummagnetisierungsschleife“ genannt werden, denn die Hystereseverluste sind nur ein Anteil.
Die Hysteseschleifen (oder besser jetzt „Ummagnetisierungsschleifen“ genannt) sowie die zugehörigen Zeitverläufe der Induktion B(t) (bzw. der Spannung u1(t) ) und der magnetischen Feldstärke H(t) (bzw. des Leerlaufstromes i1l(t) ) sind in den folgenden Bildern dargestellt.
 
Verbindet man die Endpunkte der partiellen Ummagnetisierungsschleifen, so erhält man die sogenannte Kommutierungskurve als eindeutige Kennlinie. Für beide Transformatorkerne sind die Kommutierungskurven im Bild dargestellt. Beim Eisenkern Dynamoblech/Stahl ist zu beachten, dass hier eine Überlagerung der Magnetisierungskennlinien zweier verschiedener Werkstoffe bei gleichzeitiger Störung der Induktionsausbildung infolge Flussverdrängung im Stahlstück erfolgt ist.
 
Die Kommutierungskurve liefert uns den nichtlinearen zeitlichen Verlauf des Magnetisierungsstromes iµ(t) (bzw. Hµ(t)), der mit der sinusförmigen Induktion B(t) in Phase ist bzw. der Spannung u1(t) um 90° nacheilt. Die Hysteresis, d. h. das Nacheilen des Leerlaufstromes i1l gegenüber der Induktion B(t) wird durch die Wirkkomponente iνH des Leerlaufstromes verursacht und diese erfasst den Energieverlust, der durch das Verschieben bzw. Umklappen der Blochwände (Ausrichten der Elementarmagnete im Kernmaterial bei wechselnder Magnetisierung) aufgewandt werden muss. Dieser Komponente iνH überlagert sich ein zweiter Anteil iνWb, der durch die Wirbelströme bedingt und mit der Spannung u1(t) in Phase ist und gegenüber der Induktion B(t) um 90° vorauseilt. Die parameter-t-freie Darstellung der Kennlinie iνWb(u1) ergibt bei rein sinusförmigen Größen eine Ellipse, die sich der Hystereseschleife iµ(u1) überlagert und diese zur Ummagnetisierungsschleife aufweitet.
Der nichtsinusförmige Leerlaufstrom i1l ergibt sich aus der Überlagerung des nichtsinusförmigen und impulsartigen Magnetisierungsstromes iµ (bzw. Hµ(t)) bei Aussteuerung der -Kennlinie in die Sättigung und des um 90° vorauseilenden Eisenverluststromes iν mit seinen durch die Hysterese und die Wirbelströme bedingten Anteilen
2.9-(9)
Der Maximalwert des Magnetisierungsstromes wird offensichtlich über die nichtlineare Kommutierungskennlinie durch den zugehörigen Spitzenwert der magnetischen Feldstärke (Index steht auch für Sättigungswert) festgelegt. Der Maximalwert des cosinusförmigen vorauseilenden Eisenverluststromes wird dagegen durch den Maximalwert der Koerzitivfeldstärke bestimmt; denn wenn der Magnetisierungsstrom iµ(t) (bzw. Hµ(t)) sein Maximum erreicht, ist der Eisenverluststrom iν = 0 (bzw. HK = 0).
Ausgehend von diesen Überlegungen wurde die Konstruktion des nichtsinusförmigen Leerlaufstromes i1l(t) (bzw. der magnetischen Feldstärke H(t) ) aus dem zeitlichen Verlauf des impulsartigen Magnetisierungsstromes iµ(t) (bzw. der zugehörigen Feldstärke Hµ(t) ) und aus dem cosinusförmigen Verlauf des Eisenverluststromes iν(t) (bzw. der zugehörigen Feldstärke HK(t)) im Bild (Konstruktion des nichtsinusförmigen Leerlaufstromes i1l(t)) für den Transformator mit dem Kernmaterial Dynamoblech/Stahl bei einer sinusförmigen Induktion mit vorgenommen.
 
Der zweite Teil unserer Arbeitshypothese ordnet der Koerzitivfeldstärke einen bestimmenden Einfluss in gewissen Grenzen auf den Maximalwert des Eisenverluststromes zu und legt den Gedanken nahe, dass die Energiedichte wFe der Fläche der Ummagnetisierungsschleife entspricht und näherungsweise über die Formel für die Ellipsenfläche
2.9-(10)
berechnet werden kann.
Bleibt man im Geltungsbereich der symbolischen Methode, so folgt aus
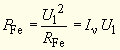2.9-(10.1)
2.9-(10.2)
und
2.9-(10.3)
 
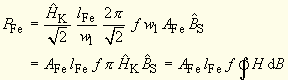2.9-(10.4)
 
für die Fläche der Ummagnetisierungsschleife die Gleichung 2.9-(10)
 
Warum nur in Grenzen? Die Berechnung von AUmmag über die Ellipsenfläche setzt voraus, dass die partiellen Hysterese(-verlust)schleifen durch Ellipsen approximiert werden können. Diese Voraussetzung ist nur für kleine Hystereseschleifen erfüllt und kann durch das Verhältnis eingegrenzt werden. Für die Frequenz f = 50 Hz und Sättigungsinduktionswerten übersteigen die Hystereseverluste die Wirbelstromverluste bei weitem, d.h. die Hystereseschleife besitzt von Haus aus eine ausgeprägte Spitze (siehe Ausdrucke der Ummagnetisierungsschleifen für Dynamoblech/Stahl und für Dynamoblech), deren Flächenanteil einen maßgeblichen Beitrag zu den Ummagnetisierungsverlusten beisteuert. Gemäß Gl. 2.9-(10) kann man die Ummagnetisierungsfläche in eine äquivalente Ellipsenfläche umrechnen, und so zu den tatsächlich gemessenen Eisenverlusten gelangen. Bei vorgegebener Aussteuerung wird allerdings dann zwangsläufig der sich aus der Ummagnetisierungsschleife ergebende Maximalwert der Koerzitivfeldstärke in einen äquivalenten Maximalwert umgerechnet.

Erst ab Frequenzen erreichen die Wirbelstromverluste die Größenordnung der Hystereseverluste und für dominieren diese, wie Ergebnisse des Versuches GET14 zeigen. Dann wird die Ummagnetisierungsschleife wieder „ellipsen“-ähnlicher, d.h. das Verhältnis gestaltet sich nun günstiger und die Formel für die Ellipsenfläche zur Berechnung der Energiedichte wm der Ummagnetisierungsschleife liefert wieder annehmbare Ergebnisse (im Rahmen einer 10%igen Genauigkeitsklasse) im Vergleich zu den tatsächlich gemessenen Eisenverlusten.

Die vorausgegangenen Betrachtungen ermöglichen uns nun, eine Einschätzung der Näherung bei der Anwendung der symbolischen Methode auf die Messergebnisse beim Leerlaufversuch zu geben.

 
Worin besteht der Fehler bei der Berechnung des Magnetisierungsstromes Iµ ?
 
Konstruktion des Leerlaufstromes aus der Grundwelle und der dritten Harmonischen Vergleich mit dem tatsächlichen Verlauf des Leerlaufstromes
Bild: Verlauf des Leerlaufstromes für eine Halbperiode
 
Der zeitliche Verlauf des Leerlaufstromes i1l(t) ist, wie wir gesehen haben, nichtsinusförmig, aber sein Effektivwert I1l kann mit einem sogenannten Echt-Effektivwertmesser bezogen auf die Periodendauer T der Grundwelle gemessen werden. Aus der eindeutigen Kommutierungskurve können wir den zeitlichen Verlauf des impulsartigen Magnetisierungsstromes iµ(t) konstruieren, der wegen iµ(t+T/2) = -iµ(t) ungeradzahlige Harmonische (3., 5., 7., 9. Harmonische usw.) enthalten wird. Dieser nichtsinusförmige Magnetisierungsstrom iµ(t) besitzt ebenfalls einen Effektivwert Iµ:
2.9-(11)
2.9-(11.1)
der bei Anwendung der Formel
2.9-(12)
die nur für rein sinusförmige Größen (symbolische Methode!) gilt, offensichtlich durch einen gleich großen sinusförmigen Magnetisierungsstrom I'µ(T) mit gleicher Periodendauer T der Grundwelle ersetzt wird. Der zeitliche Verlauf des Eisenverluststromes iν wird sinusförmig vorausgesetzt.
Beachte: Die Stromoberschwingungen treten bei Betrieb des Transformators am starren Netz nur in der Primärseite auf, denn der sinusförmige Fluss Φh induziert in der Sekundärwicklung eine sinusförmige Spannung u2(t) , die bei linearem Lastfall auch einen sinusförmigen Strom i2(t) antreibt. Eine besondere Bedeutung hat dabei die 3. Harmonische (größte Amplitude der Oberwellen).
 
Wir halten also fest, dass die Fläche der Ummagnetisierungsschleife (Gleichung 2.9-(10))
die gesamte Energiedichte wFe der Eisenverluste PFe beinhaltet und nicht nur den Anteil der Hystereseverluste PH widerspiegelt siehe Gleichung 2.9-(10.5):
2.9-(10.5)
Die Rechteckregel für die numerische Integration, angewandt auf die Ummagnetisierungsschleife, ergibt (unter Nutzung ihrer Symmetrie zur H-Achse)
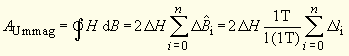2.9-(10.6)
nach Auszählung der Ummagnetisierungschleifen zum Kern Dynamoblech/Stahl folgende Ergebnisse für die:
Eisenverluste bei zwei Aussteuerungen:
 
Messwerte zum Vergleich
 
Für den Kern Dynamoblech (Dbl) erhält man nachstehende Ergebnisse für
Eisenverluste bei Aussteuerung:
Die Planimeterwerte sind in guter Übereinstimmung mit den Messwerten.
 
Eine Messung der Hystereseverluste PH allein ist nur aus der statischen Hystereseschleife (Gleichstromaufnahme) exakt richtig bzw. bei einer dynamischen Wechselstromaufnahme mit sehr kleinen Frequenzen f möglich, wenn gesichert ist, dass
PH >> Pwb
gilt. Jede Frequenz- und/oder Induktionserhöhung führt automatisch zu einer Vergrößerung der Koerzitivfeldstärke und damit zu einer Aufweitung der Ummagnetisierungsschleife, weil beide Größen in ihrer quadratischen Abhängigkeit die Wirbelstromverluste erhöhen.
In der gängigen Literatur zu diesem Thema wird bedauerlicherweise kaum auf diesen Umstand hingewiesen, sondern meist die Ummagnetisierungsschleife mit der Hystereseschleife gleich gesetzt und nur von den Hystereseverlusten PH gesprochen, ohne dass bedacht wird, dass auch die Wirbelstromverluste Pwb ebenfalls Einfluss auf die Gestalt der Ummagnetisierungsschleife nehmen. Die u1/iνwb-Kennlinie stellt eine Ellipse dar, die sich der reinen -Hystereseschleife überlagert und diese zur Ummagnetisierungsschleife aufweitet. Manche Autoren sprechen dann von der dynamischen Magnetisierungskennlinie(schleife) (Einschluss der Wirbelstromverluste) im Gegensatz zur (einfachen) Hystereseschleife.