Kompendium

Übertragungsfunktion


Mit der Zerlegung einer nichtsinusförmigen periodischen Generatorspannung in eine Fourier-Reihe (Gleichung (21)) kann die Wirkung jeder Harmonischen für sich im Netz mit den bekannten Methoden der Wechselstromlehre berechnet werden.
Infolge der unterschiedlichen Frequenzabhängigkeit der Impedanz der Bauelemente L, C im Netz kommt es zu sogenannten linearen Verzerrungen.
Eine Ursache (Eingangsgröße)

 
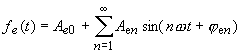(47)
führe zur Wirkung (Ausgangsgröße)  
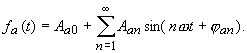(48)
Die Verrechnung des Eingangsspektrums Aen, φen zum Ausgangsspektrum Aan, φ an erfolgt über die sogenannte Übertragungsfunktion der Schaltung (des Systems). Sie ist allgemein das Verhältnis des Zeigers einer Ausgangsgröße zum Zeiger der ihn verursachenden Eingangsgröße:  
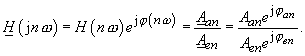(49)
Die Übertragungsfunktion H(jnω ) leitet man mit den bekannten Methoden der Wechselstromlehre aus der Schaltung ab.
Bei den Herleitungen der Übertragungsfunktion ist zu beachten, dass die komplexen Widerstände der Blindelemente nun mit 		 
 
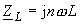bzw.  
 
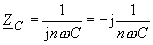einzusetzen sind.