Experimentieranleitung

Wechselspannung an Reihenschwingkreis

Lernziel:

Beobachtung und Bewertung der Zusammenhänge beim Zuschalten einer Wechselspannung an einen Reihenschwingkreis bei Variation von R und ω₀

Lerninhalt:

Beim Zuschalten einer Wechselspannung u_e(t) = Û_esin(ω_et + 90°) zum Zeitpunkt t = 0 an einen Reihenschwingkreis lautet die Stromfunktion für den Schwingfall (R < R_Grenz)

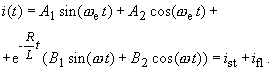
(vgl. MATHCAD-Arbeitsblatt zum Beispiel 8).
Die Terme mit A₁ und A₂ lassen sich zur bekannten stationären Lösung (komplexe Wechselstromrechnung) zusammenfassen:

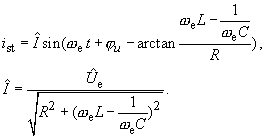
Wegen des Schaltverhaltens der Spule ist i(t=0) = 0.
Für
ist ab t = 100 ms der flüchtige Stromanteil vernachlässigbar. Der stationäre Stromanteil eilt für ω₀ > ω_e der Spannung nach (ohmsch-induktives Verhalten des Schwingkreises).
Für R = R_Grenz (aperiodischer Grenzfall) lautet die Stromfunktion
i(t) = A₁sin(ω_et) + A₂cos(ω_et) + e^-δt(B₃ + tB₄).
Für R > R_Grenz (aperiodischer Fall) lautet die Stromfunktion

Dabei sind
Wegen der großen Abklingkonstanten δ ist der flüchtige Stromanteil kaum auszumachen.

Handlungsaufforderung:

Bewerten Sie die Verhältnisse bei R < R_Grenz und ω₀ < ω_e. Passen Sie den Strom- und Zeitmaßstab an!
Für R = 0 Ω entsteht eine Schwebung mit den Kreisfrequenzen ω₀, ω_e.
Was passiert bei ω₀ = ω_e?