Fourier, Jean-Baptiste-Joseph de

(Mathematiker, mathematischer Physiker)

geb.: 21.03.1768 Auxerre,
gest.: 16.05.1830 Paris;
Fourier war einer der Begründer der mathematischen Physik, entwickelte die Grundlagen der mathematischen Theorie der Wärmeleitung, leistete Beiträge zur Theorie der partiellen Differentialgleichungen und führte Untersuchungen über trigonometrische Reihen durch. Fourier, seit dem 9. Lebensjahr Waise, wurde an der städtischen Militärschule Auxerre untergebracht, wo er seine Liebe für die Mathematik entdeckte. Er wollte der Artillerie oder den Pionieren beitreten, wurde aber trotz Befürwortung A.-M. Legendres abgelehnt, da er nicht von Adel war. Fourier ging an die Benediktinerschule nach St. Benoit-sur-Loire und hoffte, seinem Spezialinteresse später in einem Pariser Seminar nachgehen zu können. Die Realisierung des Plans scheiterte durch die Französische Revolution.
Fourier kehrte 1789 nach Auxerre zurück und wurde Lehrer für Mathematik, unterrichtete aber auch Rhetorik, Geschichte und Philosophie. Ende 1789 las er vor der Akademie der Wissenschaften in Paris eine Abhandlung über die Auflösung der numerischen Gleichungen aller Grade, die große Anerkennung fand, aber in den Unruhen des Revolutionsjahres verschwand. Während der Revolution wurde er 1794 verhaftet, aber nach der Hinrichtung Robespierres (20. 7. 1794) wieder freigelassen. Fourier ging als Lehrer an die Ecole Normale, die im gleiche Jahr eröffnet, aber bald wieder geschlossen wurde. 1795 übernahm er eine Stelle an der Ecole Polytechnique und unterstützte J. L. Lagrange und G. Monge in der Lehre. Doch auch hier wurde er ein Opfer der Reaktion und erneut verhaftet, aber bald wieder freigelassen.
Auf Vorschlag G. Monges nahm Fourier 1798 an dem Feldzug Napoleons (1769 - 1821) nach Ägypten teil. Er wurde dort Sekretär des neugegründeten Institut dEgypte. Fourier leitete Verhandlungen, hatte verschiedene diplomatische Ämter inne und betrieb weiter seine Forschungen. Es entstanden hier die Arbeiten über die Auflösung der algebraischen Gleichungen, über den Beweis eines neuen algebraischen Satzes, über allgemeine Mechanik, über die Konstruktion eines Aquäduktes, über die Oasen u.a.
Nach seiner Rückkehr nach Frankreich 1801 wollte Fourier seine Arbeit an der Ecole Polytechnique wieder aufnehmen, aber Napoleon ernannte ihn zum Präfekten des Departements d'Isere mit dem Sitz in Grenoble (1802). Die administrativen Arbeiten unterbrachen kaum Fouriers Forschungen. Er verfasste 1807 "die Mathematische Theorie der Wärme" und legte diese Arbeit der Akademie der Wissenschaften vor. Von den Gutachtern wurde dieses Werk günstig aufgenommen, aber Lagrange missfiel es, da es seinen eigenen Berechnungen widersprach. Die Abhandlung wurde damals nicht veröffentlicht. 1810 wurde eine Preisaufgabe über Wärmediffusion ausgeschrieben, an der sich auch Fourier beteiligte. Er sandte eine überarbeitete Version seiner 1807 verfassten Arbeit ein und gewann den Wettbewerb. Napoleon verlieh Fourier 1815 den Grafentitel und ernannte ihn zum Präfekten des Departements de Rhone mit Sitz in Lyon. Fourier verzichtete auf den Titel und die Präfektur und ging nach Paris, um sich ganz seinen Forschungen zu widmen. Dort wurde er Direktor des Büros für Statistik und 1817 in die wieder errichtete Akademie der Wissenschaften aufgenommen. 1822 vollendete Fourier sein Hauptwerk "Theorie analytique de la chaleur", in dem er eine Herleitung der Differentialgleichung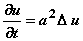

für die Temperaturverteilung u(x, y, t) in einem homogenen Körper gab. In dem gegenüber früheren Darstellungen erweiterten mathematischen Teil traten auch die nach ihm benannten Fourierschen Reihen und das Fouriersche Integral für die Entwicklung einer beliebigen periodischen bzw. nichtperiodischen Funktion auf. In einem weiteren Kapitel behandelte Fourier die Entwicklung einer beliebigen Funktion in eine trigonometrische Reihe und gab die sogenannten Fourier-Koeffizienten für die Reihenentwicklung an. Es gelang Fourier allerdings noch nicht, strenge Konvergenzbeweise zu führen und genauer zu bestimmen, welche Funktionen durch eine Reihe darstellbar sind. Das Buch brachte auch eine gewisse Entscheidung des Streites um das Problem der schwingenden Saite, dem viele Mathematiker ihre Aufmerksamkeit gewidmet hatten. Eine erweiterte Bearbeitung der physikalischen Aspekte für diese Abhandlung, auch für ein gesondertes Werk "Theorie physique de la chaleur" war geplant, aber sie wurde nie zu Ende geführt. Die Theorie der Fourier-Reihen bzw. die Theorie der aus dem Fourier-Integral hervorgehenden Fourier-Transformation fanden zahlreiche Anwendungen in Physik und Technik. Außerdem hat erstere wertvolle Anregungen für die Entwicklung mehrerer Disziplinen, wie Mengenlehre und Funktionalanalysis, geliefert, während letztere fundamentale Bedeutung in der Wahrscheinlichkeitsrechnung und bei der Lösung von Differentialgleichungen erlangte. Fourier bekam 1822 die einflussreiche Stellung eines Sekretärs auf Lebenszeit an der Pariser Akademie der Wissenschaften.