Euler, Leonhardgeb.: 15.04.1707 Basel; gest.: 18.09.1783 St. Petersburg; |

|
Nach Lateinschulbesuch und Privatunterricht
wurde der Pfarrerssohn schon 1720 an der philosophischen Fakultät der
Universität Basel und 1723 an deren theologischer Fakultät immatrikuliert.
Vorlesungen von Johann I Bernoulli führten ihn zur Mathematik. 1727 folgte
er Daniel und Nikolaus II Bernoulli den Söhnen seines Lehrers, nach Petersburg
an die neu gegründete Akademie, wurde dort 1731 Professor für Physik und
übernahm 1733 die Professur für Mathematik. Innenpolitische Wirren nach
dem Tode der Zarin Anna I. (1693 - 1740) bewogen Euler, 1741 einem Ruf
Friedrich Il. (1712 - 1786) an die Berliner Akademie zu folgen, deren
Direktor der mathematischen Klasse er ab 1746 wurde und die er nach dem
Tode ihres Präsidenten P. L. M. de Maupertius de facto, aber nicht nominell,
leitete. Fortgesetzte Differenzen mit dem König bewogen Euler, 1766 nach
St. Petersburg zurückzugehen, wo er, obwohl kurz nach seiner Ankunft erblindet,
bis zu seinem Tode unermüdlich schöpferisch tätig war.
Euler erzielte bahnbrechende Resultate in allen mathematischen Disziplinen und war die prägende Gestalt der Mathematik des 18. Jh.; er war aber auch ein bedeutender Vertreter einer mathematisch orientierten Naturwissenschaft. Auf ihn gehen grundlegende Methoden und Resultate in der Mechanik, der Astronomie, der Geodäsie und Kartographie, der Ballistik, der Navigation, der Optik, der Schiffswissenschaft und der Theorie der Turbinen zurück. Sowohl in Bezug auf inhaltliche Breite und Vielfalt als auch bezüglich des Umfangs hat Euler ein gigantisches Werk hinterlassen. Obwohl nie direkt akademischer Lehrer, haben ihn Generationen von Mathematikern als ihren Lehrer betrachtet. Diesen Einfluss gewann er durch zahlreiche Lehrbücher: Euler ist der Begründer des modernen Lehrbuchs, das systematisch von den einfachen Grundlagen bis an die Front der Forschung führt. Er schrieb u.a. Bücher über Mechanik, Variationsrechnung, eine Einführung in die Analysis des Unendlichen, ein Werk über Differentialrechnung, eine dreibändige Integralrechnung und eine Einführung in die Algebra. In allen diesen Büchern hat Euler neben Resultaten seiner Vorgänger zahlreiche eigene Ergebnisse im Zusammenhang dargestellt und dabei mancher Disziplin einen (inhaltlich und methodisch) noch heute gebräuchlichen Aufbau gegeben. Viele seiner Bezeichnungen haben sich eingebürgert, wie die der trigonometrischen Funktionen, das Funktionssymbol f(x), die Buchstaben e für die Basis der natürlichen Logarithmen und i für die imaginäre Einheit, die Zeichen D für Differenz und S für Summe. Einen beträchtlichen Anteil in Eulers Schaffen nahm die Analysis ein. Hatten I. Newton und die Bernoullis die Analysis noch eng mit der geometrischen Anschauung verbunden, so hat Euler den Funktionsbegriff als zentralen Begriff in den Mittelpunkt gerückt. Dabei kam er bis zum Verständnis einer Funktion als Zuordnung zweier Zahlenmengen, wie es später durch P. G. L. Dirichlet zum Allgemeingut der Mathematiker geworden ist. Das Hauptmittel zur Darstellung und Untersuchung von Funktionen ist bei Euler die Potenzreihe. Er entwickelte die elementaren Funktionen, untersuchte ihre Eigenschaften und erkannte grundlegende Zusammenhänge zwischen ihnen, z. B.
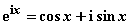
Damit schuf er die Ausgangspunkte einer allgemeinen Funktionentheorie, wie sie später von A. L. Cauchy , B. Riemann, C. Weierstrass u.a. geschaffen worden ist.
Euler benutzte zur Darstellung von Funktionen auch unendliche Produkte und Reihen von Partialbrüchen, Verfahren also, die im 19. Jh. durch Weierstrass und G. Mittag-Leffler ausgebaut worden sind. Euler führte durch Integration von Funktionen oder von Differentialgleichungen neue interessante Klassen transzendenter Funktionen ein, wie die Gamma-Funktion, die Beta-Funktionen und die Zylinderfunktionen erster Art. Bei Differentialgleichungen geht der Ansatz
Euler erzielte bahnbrechende Resultate in allen mathematischen Disziplinen und war die prägende Gestalt der Mathematik des 18. Jh.; er war aber auch ein bedeutender Vertreter einer mathematisch orientierten Naturwissenschaft. Auf ihn gehen grundlegende Methoden und Resultate in der Mechanik, der Astronomie, der Geodäsie und Kartographie, der Ballistik, der Navigation, der Optik, der Schiffswissenschaft und der Theorie der Turbinen zurück. Sowohl in Bezug auf inhaltliche Breite und Vielfalt als auch bezüglich des Umfangs hat Euler ein gigantisches Werk hinterlassen. Obwohl nie direkt akademischer Lehrer, haben ihn Generationen von Mathematikern als ihren Lehrer betrachtet. Diesen Einfluss gewann er durch zahlreiche Lehrbücher: Euler ist der Begründer des modernen Lehrbuchs, das systematisch von den einfachen Grundlagen bis an die Front der Forschung führt. Er schrieb u.a. Bücher über Mechanik, Variationsrechnung, eine Einführung in die Analysis des Unendlichen, ein Werk über Differentialrechnung, eine dreibändige Integralrechnung und eine Einführung in die Algebra. In allen diesen Büchern hat Euler neben Resultaten seiner Vorgänger zahlreiche eigene Ergebnisse im Zusammenhang dargestellt und dabei mancher Disziplin einen (inhaltlich und methodisch) noch heute gebräuchlichen Aufbau gegeben. Viele seiner Bezeichnungen haben sich eingebürgert, wie die der trigonometrischen Funktionen, das Funktionssymbol f(x), die Buchstaben e für die Basis der natürlichen Logarithmen und i für die imaginäre Einheit, die Zeichen D für Differenz und S für Summe. Einen beträchtlichen Anteil in Eulers Schaffen nahm die Analysis ein. Hatten I. Newton und die Bernoullis die Analysis noch eng mit der geometrischen Anschauung verbunden, so hat Euler den Funktionsbegriff als zentralen Begriff in den Mittelpunkt gerückt. Dabei kam er bis zum Verständnis einer Funktion als Zuordnung zweier Zahlenmengen, wie es später durch P. G. L. Dirichlet zum Allgemeingut der Mathematiker geworden ist. Das Hauptmittel zur Darstellung und Untersuchung von Funktionen ist bei Euler die Potenzreihe. Er entwickelte die elementaren Funktionen, untersuchte ihre Eigenschaften und erkannte grundlegende Zusammenhänge zwischen ihnen, z. B.
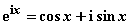
Damit schuf er die Ausgangspunkte einer allgemeinen Funktionentheorie, wie sie später von A. L. Cauchy , B. Riemann, C. Weierstrass u.a. geschaffen worden ist.
Euler benutzte zur Darstellung von Funktionen auch unendliche Produkte und Reihen von Partialbrüchen, Verfahren also, die im 19. Jh. durch Weierstrass und G. Mittag-Leffler ausgebaut worden sind. Euler führte durch Integration von Funktionen oder von Differentialgleichungen neue interessante Klassen transzendenter Funktionen ein, wie die Gamma-Funktion, die Beta-Funktionen und die Zylinderfunktionen erster Art. Bei Differentialgleichungen geht der Ansatz
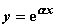
für die Lösung der homogenen linearen Differentialgleichung mit konstanten Koeffizienten auf Euler zurück; die zugehörige inhomogene Gleichung löste er mit der Methode des integrierenden Faktors, die er auch in vielen anderen Fällen erfolgreich einsetzte. Für die Anwendungen bedeutsam war seine Polygonzugmethode zur numerischen Lösung des Anfangswertproblems:

Viele wichtige Resultate zur Integration partieller Differentialgleichungen sind in Eulers Arbeiten zur Mechanik enthalten. So ging aus einem Streit zwischen Euler, J. R. dŽAlembert und Daniel I Bernoulli um die Frage nach den möglichen Lösungen der Differentialgleichung der schwingenden Saite das Problem hervor, welche Funktionen durch trigonometrische Reihen darstellbar sind. Dieses Problem hat im 19. Jh. mit der Entwicklung der Theorie der Fourier-Reihen zur Herausarbeitung bzw. Präzisierung grundlegender Begriffe der Mathematik, wie Funktion, Integral, reelle Zahl, Punktmenge und transfinite Ordinalzahl, geführt. Während vor Euler spezielle Variationsprobleme mit Kunstgriffen behandelt wurden, die dem jeweiligen Spezialfall angepasst waren, entwickelte Euler die Variationsrechnung zu einem eigenständigen Zweig der Analysis. Er formulierte das allgemeine Variationsproblem
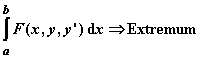
und leitete als notwendige Bedingung für eine Extremale die nach ihm benannte Differentialgleichung
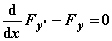
her.
Mit zahlreichen originellen Beispielen veranschaulichte er seine Methode. In der Theorie der divergenten Reihe hat Euler Ideen antizipiert, deren Wert über ein Jh. total verkannt erst zu Beginn des 20. Jh. durch Forschungen von E. Cesaro, E. Borel u.a. gewürdigt werden konnte.
I. Newton hatte 1687 in seinen "Principia" die Grundlagen der klassischen Mechanik gelegt. Aus heutiger Sicht betrifft dies aber nur den physikalischen Inhalt: Die Darstellung war noch rein geometrisch und daher schwerfällig. Euler hat es erstmals unternommen, die genialen Ansätze Newtons mit der neuen Analysis zu verbinden. Bei ihm tritt die Bewegungsgleichung - eine Differentialgleichung - in den Mittelpunkt der Betrachtung; aus ihr wird dann alles rein analytisch abgeleitet. Später hat Euler diese Betrachtungsweise vom Massenpunkt auf Massenpunktsysteme und starre Körper (Kreiseltheorie) ausgedehnt. Er erkannte den Drehimpulssatz als unabhängiges Prinzip. Von ihm stammt auch der Begriff der idealen Flüssigkeit und die Grundgleichungen der Bewegung einer idealen Flüssigkeit im Raum.
Die Lösung einer Reihe von Problemen der Elastizitätstheorie geht auf Euler zurück: Die Behandlung der schwingenden Saite und kreisrunder Membranen, das Knicklastproblem u.a. In seiner Mondtheorie gab er eine sehr gute Näherungslösung für das Drei-Körper-Problem. Eine Reihe von Untersuchungen führte er bis zur prinzipiellen Möglichkeit einer technischen Anwendung (Turbinentheorie, Schiffsantrieb, Schiffsstabilität, Fragen der äußeren Ballistik u.a.). In der Algebra formulierte Euler erstmalig den Satz, dass die Wurzeln eines Polynoms alle von der Form a + ib sind. Vorher hatte man angenommen, dass außer diesen Zahlen noch imaginäre Zahlen höherer Art als Wurzeln vorkommen können, die sich nicht auf die Form a + ib bringen lassen.
In der Geometrie hat Euler eine Vielzahl von Resultaten durch Anwendung der Methoden der Algebra und der Analysis erzielt, insbesondere zur Differentialgeometrie der Kurven und Flächen. Zwei singuläre Ergebnisse Eulers, die Lösung des sogenannten Königsberger Brückenproblems und die nach ihm benannte Polyederformel, gehören in die Graphentheorie bzw. kombinatorische Topologie, die erst Ende des 19./ Anfang des 20. Jh. zu eigenständigen mathematischen Disziplinen ausgebaut wurden.
In der Zahlentheorie wandte sich Euler zunächst den von P. Fermat hinterlassenen unbewiesenen Vermutungen zu. Er bewies den sogenannten Kleinen Fermatschen Satz, dass
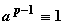
(mod p) ist für Primzahlen p und dazu teilerfremdes a, und verallgemeinerte ihn durch Einführung der nach Euler benannten Funktion j(n), die die Anzahl der zu n teilerfremden Zahlen < n angibt. Die Behauptung Fermats, die Zahlen
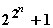 seien für alle n
= 0, 1, 2, ... Primzahlen, widerlegte Euler, indem er zeigte, dass
seien für alle n
= 0, 1, 2, ... Primzahlen, widerlegte Euler, indem er zeigte, dass
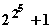 den Teiler 641 hat. Der bis heute für
beliebiges n noch unbewiesene Große Fermatsche Satz, dass die diophantische
Gleichung
den Teiler 641 hat. Der bis heute für
beliebiges n noch unbewiesene Große Fermatsche Satz, dass die diophantische
Gleichung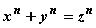
für n > 2 keine Lösung in ganzen Zahlen habe, wurde von Euler für den Fall n = 3 verifiziert und damit eine Entwicklungsrichtung eröffnet, die für die Herausbildung der algebraischen Zahlentheorie von großer Bedeutung war. Euler führte die Zeta-Funktion
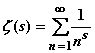
ein, fand ihre Funktionalgleichung und leitete die berühmte Produktdarstellung
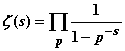
her. Diese Funktion, deren Verhalten auch heute noch nicht in allen Einzelheiten geklärt ist und auf die sich z. B. die berühmte Riemannsche Vermutung bezieht, dass ihre komplexen Nullstellen alle den Realteil 1/2 haben, spielt eine entscheidende Rolle in der analytischen Zahlentheorie. Aus umfangreichen Zahlenrechnungen erriet Euler das quadratische Reziprozitätsgesetz, konnte es allerdings nicht beweisen. A. M. Legendre und C. F. Gauß haben es unabhängig von Euler wiederentdeckt; ein vollständiger Beweis dieses Gesetzes war eine der ersten wissenschaftlichen Großtaten des jungen Gauß. Viele Ergebnisse Eulers können hier nicht im Detail erwähnt werden. Ihre Fülle wird dadurch angedeutet, dass über 50 Begriffe, Sätze und Verfahren in der Mathematik und Mechanik nach Euler benannt wurden.