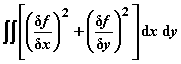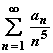Dirichlet, Johann Peter Gustav
(eigentlich Lejeune Dirichlet, J. P. G.)
geb.: 13.02.1805 Düren (bei Aachen)
gest.: 05.05.1859 Göttingen |

|
Dirichlet war Sohn eines Postkommissars von Düren, dessen
französische oder wallonische Vorfahren aus Richelet bei Verviers (Belgien)
stammten; der Name "Lejeune Dirichlet" könnte also "der junge Mann aus Richelet"
bedeuten. Seine mathematische Ausbildung erhielt Dirichlet in Paris, wo
er sich 1822 - 1826 aufhielt und ständigen Kontakt mit führenden französischen
Mathematikern hatte, insbesondere mit J. J. Fourier, S. D. Poisson und S.
F. Lacroix. 1825 bewies er ein wesentliches Teilresultat für die Bestätigung
der Fermatschen Vermutung für n
= 5, d. h. dafür, dass keine natürlichen Zahlen x,
y, z mit
existieren; diese Methoden hat später A. M. Legendre
aufgegriffen und zum vollen Beweis dieser Vermutung für n = 5 fortgeführt.
1827 erhielt Dirichlet von der Universität Bonn den Dr. h.c. und wurde,
gefördert durch A. von Humboldt (1769 - 1859), Privatdozent und außerordentlicher
Professor an der Universität Breslau (Wroclaw). 1829 ging Dirichlet als
Privatdozent an die Universität Berlin, wo er 1831 außerordentlicher Professor
und 1839 ordentlicher Professor wurde. 1855 folgte er einem Ruf an die Universität
Göttingen als Nachfolger von C. F. Gauß. Dirichlet lieferte bahnbrechende
Arbeiten zur Mathematik und zur mathematischen Physik, die von Gauß als
"Juwelen" bezeichnet wurden, die man "nicht mit der Krämerwaage" wägt. Er
wirkte mit großem Erfolg sowohl durch seine tiefschürfenden Abhandlungen
als auch durch seine vorbildlichen Vorlesungen über damals aktuellste und
schwierigste Fragen der Mathematik und auch durch fundierte Gutachten für
die Universität und Akademien in Berlin und Göttingen. Zusammen mit C. G.
J. Jacobi leitete Dirichlet dadurch eine neue Epoche des Mathematikbetriebes
in Deutschland ein. Zu seinen Schülern gehören so bedeutende Mathematiker
wie E. E. Kummer, G. Eisenstein, L. Kronecker, B. Riemann und R. Dedekind.
In seinen Arbeiten führte Dirichlet sowohl Ideen von Gauß, dessen geniales
zahlentheoretisches Werk "Disquisitiones arithmeticae" er den Zeitgenossen
erschloss, als auch von französischen Vertretern der Analysis und der mathematischen
Physik weiter. An Fourier anknüpfend, lieferte Dirichlet einen Konvergenzbeweis
für die Entwickelbarkeit periodischer, stückweise stetiger und monotoner
Funktionen einer reellen Variablen nach trigonometrischen Funktionen. Er
löste für die Potentialgleichung von P. S. Laplace Randwertprobleme und
lieferte Beiträge zur Hydrodynamik. Dabei verwendete er das Dirichletsche
Prinzip, das die Lösung einer Randwertaufgabe durch Minimierung eines Integrals
ergibt, das bei ebenen Problemen die Form
hat, also auf eine Aufgabe der Variationsrechnung zurückführt.
Dieses Prinzip erwies sich als sehr nützlich, die damit verbundene Existenzbehauptung
für eine minimierende Lösung konnte aber erst 1899 von D. Hilbert allgemein
bewiesen werden.
Grundsätzlich neue Hilfsmittel der Analysis führte Dirichlet in die Zahlentheorie
ein, u.a. die Dirichlet-Reihen der Form
Damit gelang ihm u. a, der Beweis des Dirichletschen
Primzahlsatzes: Jede arithmetische Folge, deren Anfangsglied und Differenz
zueinander teilerfremd sind, enthält unendlich viele Primzahlen. Er bestimmte
damit auch explizit die Klassenzahlformeln für binäre quadratische Formen.
Wesentliche und abschließende Ergebnisse fand Dirichlet über Einheiten in
algebraischen Zahlkörpern endlichen Grades. |